and the distribution of digital products.
Why Some AI Power Flow Models Are Faster Than Others
:::info Authors:
(1) Mengshuo Jia, Department of Information Technology and Electrical Engineering, ETH Zürich, Physikstrasse 3, 8092, Zürich, Switzerland;
(2) Gabriela Hug, Department of Information Technology and Electrical Engineering, ETH Zürich, Physikstrasse 3, 8092, Zürich, Switzerland;
(3) Ning Zhang, Department of Electrical Engineering, Tsinghua University, Shuangqing Rd 30, 100084, Beijing, China;
(4) Zhaojian Wang, Department of Automation, Shanghai Jiao Tong University, Dongchuan Rd 800, 200240, Shanghai, China;
(5) Yi Wang, Department of Electrical and Electronic Engineering, The University of Hong Kong, Pok Fu Lam, Hong Kong, China;
(6) Chongqing Kang, Department of Electrical Engineering, Tsinghua University, Shuangqing Rd 30, 100084, Beijing, China.
:::
Table of Links2. Evaluated Methods
3. Review of Existing Experiments
4. Generalizability and Applicability Evaluations and 4.1. Predictor and Response Generalizability
4.2. Applicability to Cases with Multicollinearity and 4.3. Zero Predictor Applicability
4.4. Constant Predictor Applicability and 4.5. Normalization Applicability
5. Numerical Evaluations and 5.1. Experiment Settings
5.5. Efficiency EvaluationThe evaluation of computational efficiency in this section includes a comparison of DPFL and PPFL methods, a general review of DPFL methods, and individual examinations of specific groups of DPFL approaches.
\ 5.5.1. DPFL Performance vs. PPFL Performance
\ As illustrated in Fig. 8, the computational efficiency of PPFL methods notably outperforms that of DPFL approaches. This advantage largely stems from the inherent nature of PPFL approaches, i.e., avoiding the need for a training process, in contrast to DPFL methods. Fundamentally, the absence of training in PPFL methods is attributed to their reliance on predefined physical models of the system, assuming that all necessary physical parameters are known and accurate. However, this assumption might not always be valid, particularly in distribution grids.
\ 5.5.2. DPFL Performance: General View
\ The computational costs of the majority of DPFL methods exhibit superlinear growth with increasing system size, approaching or even exceeding quadratic growth rates, even for methods with closed-form solutions. Much of the computational effort is devoted to model fitting, particularly for DPFL methods that require tuning of hyperparameters. For instance, clustering-based methods have to tune the number of clusters by cross-validation, while ridge-regression-related methods need cross-validation to adjust the regularization factor. This tuning process can be computationally intensive, as it involves systematically searching for better hyperparameter values, which often require multiple iterations of model training and validation.
\ It is important to highlight that, aside from the DPFL methods which encountered OOT failures, several DPFL approaches, particularly in the 1354-bus-S case, showed computational times exceeding 300 seconds. Considering that the real-time dispatch in some countries operates on a five-minute cycle, these slower DPFL methods fall short of meeting the real-world computational speed requirements. Given the considerable computational burden many DPFL methods face in large systems, exploring ways to accelerate their training becomes a practical concern. However, it is crucial to clarify that not all DPFL methods suffer from excessive computational efforts. Recursive DPFL methods, in particular, demonstrate more promising speed, which will be further explained in the subsequent discussion.
\ 5.5.3. DPFL Performance: Individual View
\ In the following, we present performance analyses of particular groups of methods.
\ High-burden Methods
\ High-burden methods refer to the methods that result in OOT failures in large-scale test cases. Such a high burden is primarily due to the reliance on optimization programming techniques. Examples include LSHBLD, LSHBLE, LSWEI, SVR, SVRCCP, SVRRR, DRCXYD, DRC_XYM,
\
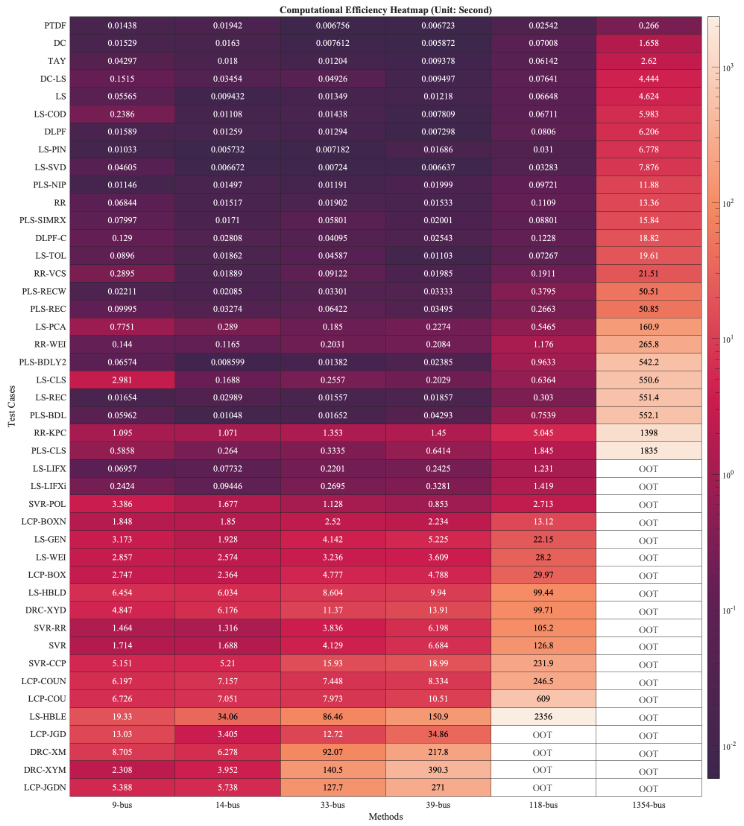
\ DRCXM, LCPBOX, LCPBOXN, LCPCOU, LCPCOUN, LCPJGD, and LCPJGDN. Even for unconstrained quadratic programming, e.g., LCPJGDN, the computational demands can quickly become overwhelming and surpass memory capabilities. For a situation where the optimization models have more complex constraints like distributionally robust or chance constraints, the computational demand can be even higher.
\ On the other hand, LSLIFX and LSLIFXi, which can also be considered as, fail in large-scale tests as they significantly increase the dataset size by dimension lifting, exceeding MATLAB’s maximum array size limitations.
\ Additionally, SVRPOL and LSGEN, the last two highburden methods, experience significant slowdowns at a system size of 1354 buses, a consequence of their specialized design of 3rd-order polynomial-kernel fitting and iterative training, respectively, as explained before.
\ Clustering-based Methods
\ Clustering-based methods like RRKPC and PSLCLS often outperform other DPFL approaches in accuracy but are notably more time-intensive. For instance, processing a 1354-bus-S case requires over 1000 seconds with these methods. The primary burden lies in the clustering phase, which is particularly demanding for large-scale datasets. This is because both RRKPC’s K-plane clustering and PSLCLS’s K-means clustering involve iterative searches for better numbers of clusters, an inherently resource-intensive process. Furthermore, these approaches require the tuning of hyperparameters through cross-validation, adding more layers of iterative computation. E.g., RR_KPC needs adjustments in both the number of clusters and regularization parameters; such a combinational search plus the clustering process significantly increases the computational demand.
\ Recursive Methods
\ Methods PLSREC and LSREC are distinguished by their recursive nature, setting them apart from techniques that rely on the entire training dataset for model fitting. Instead, PLSREC and LSREC incrementally refine the model through hundreds or thousands of updates. For instance, in the 1343-bus-S case, PLSREC begins by using 40% of the training dataset, which equates to the old dataset with 1200 data samples, to establish an initial linear model via the ordinary partial least squares approach. Subsequently, PLSREC imitates an online procedure by incorporating each new data point as it arrives, thereby updating the linear model recursively. Ultimately, PLSREC performs 1800 updates to derive the final model, which amounts to the entire training set comprising 3000 data points. Note that the entire recursive process is remarkably efficient, i.e., 50.85 seconds in total or approximately 0.028 seconds for each point-wise update for this test case. Considering a measuring time resolution of one point every half second, where five minutes yield 600 data points, these data can be recursively integrated by PLSREC in roughly 16.8 seconds using a consumer-grade laptop. This efficiency aligns well with the requirements of five-minute real-time dispatch scenarios.
\ Well-rounded Methods
\ Methods that balance high accuracy, efficiency, and practicality (where “practical” means not significantly increasing the complexity of the application) include LSCOD, DLPFC, PLSNIP, and PLSREC. While the transformationbased RR_VCS method has advantages in both accuracy and computational time, its model is challenging to apply in optimization and similar applications.
\
:::info This paper is available on arxiv under CC BY-NC-ND 4.0 Deed (Attribution-Noncommercial-Noderivs 4.0 International) license.
:::
\