and the distribution of digital products.
Redefining Anomaly Detection with Signature Isolation Forests
:::info Authors:
(1) Guillaume Staerman, INRIA, CEA, Univ. Paris-Saclay, France;
(2) Marta Campi, CERIAH, Institut de l’Audition, Institut Pasteur, France;
(3) Gareth W. Peters, Department of Statistics & Applied Probability, University of California Santa Barbara, USA.
:::
Table of Links2.1. Functional Isolation Forest
3. Signature Isolation Forest Method
4.1. Parameters Sensitivity Analysis
4.2. Advantages of (K-)SIF over FIF
4.3. Real-data Anomaly Detection Benchmark
5. Discussion & Conclusion, Impact Statements, and References
\ Appendix
A. Additional Information About the Signature
C. Additional Numerical Experiments
3. Signature Isolation Forest MethodWith Kernel Signature Isolation Forest (K-SIF), we aim to leverage the truncated kernel signature (Kiraly and Oberhauser, 2019) to overcome the linearity constraint imposed by the inner product in FIF. In contrast to FIF, which explores only one function characteristic at each node using a unique inner product with the function sampled in the dictionary, K-SIF captures significantly more information. This is achieved by computing several coefficient signatures, summarizing multiple data attributes at each node.
\ The ability to explore non-linear directions in the feature space through the kernel signature makes the algorithm more efficient for an equivalent computational cost (refer to Figure 9 in the Appendix
\ With Signature Isolation Forest (SIF), the aim is to leverage the coordinate signature and remove any restrictions imposed by FIF and K-SIF. We replace the use of a dictionary D and rely on the coordinate signature only to detect anomalies. The intuition is to provide a more straightforward, entirely data-driven solution and remove any a priori required choice.
\ The construction procedures of (K-)SIF are now described.
\
\ Splitting Criterion. The difference between a ksi-tree and a si-tree lies in the splitting criterion computed at each node of both trees. Below, we detail the splitting procedures occurring at a particular internal node for both algorithms.
\
\ The following step is to choose uniformly and at random a split value γ such that
\
\ The children datasets are given as
\
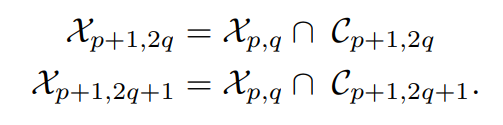
\ A ksi-tree is built by iterating this procedure until all training data curves are isolated.
\ Signature Isolation Forest. In contrast to ksi-trees, the definition of a si-tree will rely on using a different split criterion, expressed according to the following procedure. Once again, the depth of the truncation level k has to be chosen a priori, but no dictionaries nor distribution has to be set. Here, at each internal node (p, q), a coordinate (i1, . . . , iℓ) is chosen randomly and uniformly in the set
\
\ The children datasets are given as
\
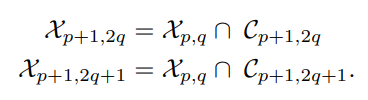
\ A si-tree is also built by iterating this procedure until all training data curves are isolated. The two algorithms of K-SIF and SIF are summarized in the Appendix B.
\
\ where c(m) is the average path length of unsuccessful searches in a binary search tree and m the size of the subsample linked to each tree.
\ Parameters of K-SIF and SIF. For both algorithms, key parameters typical of isolation forest-based methods, such as the number of trees N or the subsample size m, must be pre-selected (Liu et al., 2008). The truncated level k of the signature depth must also be chosen. In the case of K-SIF, similar to FIF, selecting a dictionary D and a distribution ν is required. We opt to implement three standard dictionaries (also utilized in FIF): ‘Brownian’, representing a traditional Brownian motion path; ‘Cosine’, employing a cosine basis; and ‘Gaussian wavelets’, utilizing a Gaussian wavelets basis. In contrast, SIF does not require any of these sensitive parameters. We follow the approach outlined in Morrill et al. (2019) to enhance the algorithms’ performance by introducing a split window parameter ω. This implies that, at each tree node, the truncated signature is computed on a randomly selected portion of the functions with a size of ⌊p/ω⌋.
\
4. Numerical ExperimentsThis section presents a series of numerical experiments supporting the proposed class of AD methods. We organize the experiments into three categories. First, a parameter sensitivity analysis sheds light on the behavior of the parameters algorithms and provides insights for achieving optimal performances. Subsequently, we compare (K-)SIF and FIF, illustrating the validity of such methods and showcasing the power of the signature in the context of AD solutions. Finally, we perform a benchmark that compares several existing AD methods on various real datasets. This benchmark aims to demonstrate the results in real applications and assess the overall performance of these algorithms relative to other AD methods documented in the literature.
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\