and the distribution of digital products.
Analyzing Optimal Signaling with Binary-outcome Experiments in Two-phase Trials
:::info Authors:
(1) Shih-Tang Su, University of Michigan, Ann Arbor ([email protected]);
(2) Vijay G. Subramanian, University of Michigan, Ann Arbor and ([email protected]);
(3) Grant Schoenebeck, University of Michigan, Ann Arbor ([email protected]).
:::
Table of Links2.1 Model of Binary-Outcome Experiments in Two-Phase Trials
3 Binary-outcome Experiments in Two-phase Trials and 3.1 Experiments with screenings
3.2 Assumptions and induced strategies
3.3 Constraints given by phase-II experiments
3.4 Persuasion ratio and the optimal signaling structure
3.5 Comparison with classical Bayesian persuasion strategies
4.2 Determined versus sender-designed experiments
4.3 Multi-phase model and classical Bayesian persuasion and References
3 Binary-outcome Experiments in Two-phase TrialsIn this section the sender’s optimization problem presented in (2) Section 2.1, is solved starting with the simplest non-trivial case. There are only two phases in the trial studied here, and from this we will develop more insight into how different types of experiments (determined versus sender-designed) influence the optimal signaling strategy of the sender. To be more specific, we will analyze how two determined experiments (in phase II) and one sender-designed experiment (in phase I) will impact the sender’s optimal signaling strategy. Before we present the general case, we discuss a subset class of two-phase trials that are similar to single-phase trials. In this class of two-phase trials, in one of the phase-II experiments, called a trivial experiment, the outcome distribution is independent of the true state. Trivial experiments [2], also called (Blackwell) non-informative experiments in some literature, are frequently used as benchmarks to compare the agents’ expected utility change under different signaling schemes/mechanisms, e.g., [22,20,21]. This two-phase model with a trivial experiment tries to capture real-world problems with one actual (and costly) experiment, e.g., clinical trials, venture capital investments, or space missions. Since the experiment is costly, a screening procedure is provided to decide whether it is worth conducting the experiment. We will then analyze the optimal signaling strategy in the general scenario, where both experiments in phase II are non-trivial.
3.1 Experiments with screeningsWe start by analyzing the sender’s optimal strategy (signaling structure) in a simple scenario where there is one non-trivial experiment conducted in phase II. The sender’s authority on choosing the probability pair (p1, p2) controls the screening process. To avoid any ambiguity, we first define what a trivial experiment is.
\
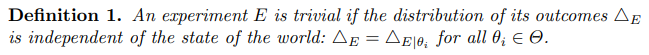
\ When a trivial experiment (in phase II) is conducted, the posterior belief of the state stays the same as the interim belief derived in (1). When there exists a trivial experiment in the two phase-II trial options, then Lemma 1 states that the sender and the receiver’s expected utility under the optimal signaling strategy is the same as in the (single-phase) classical Bayesian persuasion problem.
\ Lemma 1. When the state space is binary, both sender and receiver’s expected utilities are the same in the following two Bayesian persuasion schemes under each scheme’s optimal signaling strategy:
\
Bayesian persuasion in a single-phase trial,
\
Bayesian persuasion in a two-phase trial with a sender-designed phase-I experiment and a trivial experiment in phase II.
\ In the single-trial classical Bayesian persuasion setting, the optimal signaling strategy only mixes the two possible states in one outcome (e.g., when the prosecutor claims the suspect is guilty). On the other outcome, the sender reveals the true state with probability one (e.g., when the prosecutor says the suspect is innocent). When there is a trivial experiment in phase II, the other experiment (supposing that it will be conducted at outcome ωB) will be rendered defunct by the sender’s choice of experiments in phase I. This phenomenon occurs because the sender can always choose to reveal the true state when the non-trivial experiment is to be conducted, i.e., by setting P(θ1|EB) = 1 or P(θ2|EB) = 1; and the classical Bayesian persuasion strategy can be replicated. In essence, having a trivial experiment in the phase-II trial does not constrain the sender.
\
:::info This paper is available on arxiv under CC 4.0 license.
:::
\