and the distribution of digital products.
DM Television
Wonder3D: Textured Mesh Extraction Explained
2. Related Works
2.1. 2D Diffusion Models for 3D Generation
2.2. 3D Generative Models and 2.3. Multi-view Diffusion Models
3. Problem Formulation
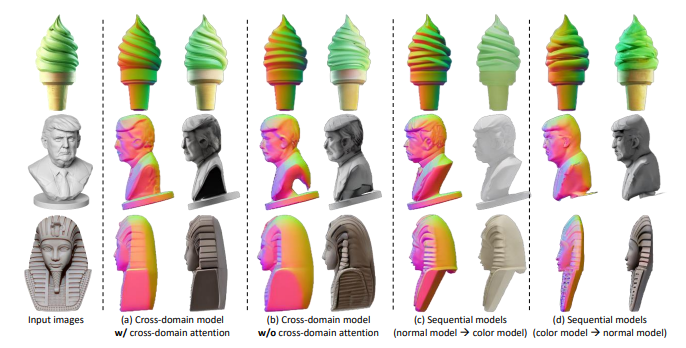
3.2. The Distribution of 3D Assets
4. Method and 4.1. Consistent Multi-view Generation
5. Experiments
5.4. Single View Reconstruction
5.5. Novel View Synthesis and 5.6. Discussions
6. Conclusions and Future Works, Acknowledgements and References
4.3. Textured Mesh ExtractionTo extract explicit 3D geometry from 2D normal maps and color images, we optimize a neural implicit signed distance field (SDF) to amalgamate all 2D generated data. Unlike alternative representations like meshes, SDF offers compactness and differentiability, making them ideal for stable optimization.
\ Nonetheless, adopting existing SDF-based reconstruction methods, such as NeuS [60], proves unviable. These methods were tailored for real-captured images and necessitate dense input views. In contrast, our generated views are relatively sparse, and the generated normal maps and color images may exhibit subtle inaccurate predictions of some pixels. Regrettably, these errors accumulate during the geometry optimization, leading to distorted geometries, outliers, and incompleteness. To overcome the challenges above, we propose a novel geometric-aware optimization scheme.
\ Optimization Objectives. With the obtained normal maps G0:N and color images H0:N , we first leverage segmentation models to segment the object masks M0:N from the normal maps or color images. Specifically, we perform the optimization by randomly sampling a batch of pixels and their corresponding rays in world space P = {gk, hk, mk, vk}, where gk is normal value of the kth sampled pixel, hk is color value of the kth pixel, mk ∈ {0, 1} is mask value of the kth pixel, and vk is the direction of the corresponding sampled kth ray, from all views at each iteration.
\

\
![Figure 6. The qualitative comparisons with baseline methods on GSO [13] dataset in terms of the reconstructed textured meshes.](https://cdn.hackernoon.com/images/fWZa4tUiBGemnqQfBGgCPf9594N2-m1a3xxi.png)
Geometry-aware Normal Loss. Thanks to the differentiable nature of SDF representation, we can easily extract normal values gˆ of the optimized SDF via calculating the second-order gradients of SDF. We maximize the similarity of the normal of SDF gˆ and our generated normal g to provide 3D geometric supervision. To tolerate trivial inaccuracies of the generated normals from different views, we introduce a geometry-aware normal loss:
\

\ The design rationale behind this approach lies in the orientation of normals, which are deliberately set to face outward, while the viewing direction is inward-facing. This configuration ensures that the angle between the normal vector and the viewing ray remains not less than 90◦ . A deviation from this criterion would imply inaccuracies in the generated normals.
\ Furthermore, it’s worth noting that a 3D point on the optimized shape can be visible from multiple distinct viewpoints, thereby being influenced by multiple normals corresponding to these views. However, if these multiple normals do not exhibit perfect consistency, the geometric supervision may become somewhat ambiguous, leading to imprecise geometry. To address this issue, rather than treating normals from different views equally, we introduce a weighting mechanism. We assign higher weights to normals that form larger angles with the viewing rays. This prioritization enhances the accuracy of our geometric supervision process.
\ Outlier-dropping Losses. Besides the normal loss, mask loss and color loss are also adopted for optimizing geometry and appearance. However, it is inevitable that there exist some inaccuracies in the masks and color images, which will accumulate in the optimization and thus cause noisy surfaces and holes.
\ trategy named outlier-dropping loss. Taking the color loss calculation as an example, instead of simply summing up the color errors of all sampled rays at each iteration, we first sort these errors in a descending order and then discard the top largest errors according to a predefined percentage. This approach is motivated by the fact that erroneous predictions lack sufficient consistency with other views, making them less amenable to effective minimization during optimization, and they often result in large errors. By implementing this strategy, the optimized geometry can eliminate incorrect isolated geometries and distorted textures.
\
:::info This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.
:::
:::info Authors:
(1) Xiaoxiao Long, The University of Hong Kong, VAST, MPI Informatik and Equal Contributions;
(2) Yuan-Chen Guo, Tsinghua University, VAST and Equal Contributions;
(3) Cheng Lin, The University of Hong Kong with Corresponding authors;
(4) Yuan Liu, The University of Hong Kong;
(5) Zhiyang Dou, The University of Hong Kong;
(6) Lingjie Liu, University of Pennsylvania;
(7) Yuexin Ma, Shanghai Tech University;
(8) Song-Hai Zhang, The University of Hong Kong;
(9) Marc Habermann, MPI Informatik;
(10) Christian Theobalt, MPI Informatik;
(11) Wenping Wang, Texas A&M University with Corresponding authors.
:::
\
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright , Central Coast Communications, Inc.