Why Lunar Clocks Tick Faster Than Earth Clocks

Abstract and 1. Introduction

2. Clock in Orbit

   2.1 Coordinate Time

   2.2 Local Frame for the Moon

3. Clock Rate Differences Between Earth and Moon

4. Clocks at Earth-Moon Lagrance Points

   4.1 Clock at Lagrange point L1

   4.2. Clock at Lagrange point L2

   4.3. Clock at Lagrange point L4 or L5

5. Conclusions

\ Appendix 1: Fermi Coordinates with Origin at the Center of the Moon

Appendix 2: Construction of Freely Falling Center of Mass Frame

Appendix 3: Equations of Motion of Earth and Moon

Appendix 4: Comparing Results in Rotating and Non-Rotating Coordinate Systems

Acknowledgments and References

\

In establishing a coordinate time on and near the Earth, two relativistic effects are compensated by adjusting the rates of standard clocks. These are (a) the gravitational potential at the geoid and (b) the second-order Doppler shift due to the Earth’s rotation. The gravitational potential at the equator can be estimated from existing models of Earth’s gravitational potential. Viewed from an Earth-centered inertial frame, the second-order Doppler shift is

\ \

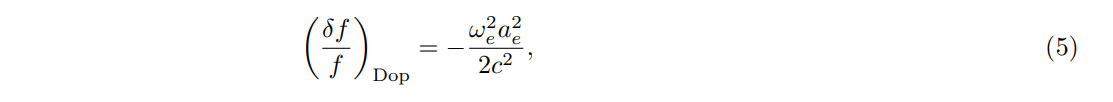
\ where ωe is Earth’s angular rotation rate and ae is the equatorial radius. Because the Earth’s geoid is nearly a surface of effective hydrostatic equilibrium, all atomic clocks on the geoid beat at equal rates, and this rate can be calculated on the Earth’s geoid at the equator. The effective potential Φ0 in Eq. (2) represents the fractional rate difference between an atomic clock at rest at infinity if the Earth were the only celestial body and an atomic clock fixed on the geoid of the rotating Earth.

\

\ With this adjustment in scale, apart from tidal effects which average to near zero, clocks at rest on the geoid beat at the rate of International Atomic Time (TAI), defined by atomic clocks at rest on the geoid. Coordinate time suitable for use in navigation and timekeeping near the Earth’s surface is then obtained by synchronizing clocks in the local inertial frame [7]. The proper time on a clock at rest on the geoid then, apart from tidal contributions, beats at the rate of coordinate time because the term Φ0 cancels the potential and second-order Doppler shifts on the geoid.

\

While the Moon appears fairly rigid, it is nearly spherical due to hydrostatic equilibrium. One can imagine a locally inertial, freely falling reference frame with its origin at the Moon’s center of mass, see Appendix 1. Near the Moon, the scalar invariant will be

\ \

\ \

:::info Authors:

(1) Neil Ashby, National Institute of Standards and Technology, Boulder, CO 80305 ([email protected]);

(2) Bijunath R. Patla, National Institute of Standards and Technology, Boulder, CO 80305 ([email protected]).

:::

:::info This paper is available on arxiv under CC0 1.0 license.

:::

\