and the distribution of digital products.
Unfair Generalization in Graph Neural Networks (GNNs)
:::info Authors:
(1) Junwei Su, Department of Computer Science, the University of Hong Kong and [email protected];
(2) Chuan Wu, Department of Computer Science, the University of Hong Kong and [email protected].
:::
Table of Links5 A Case Study on Shortest-Path Distance
6 Conclusion and Discussion, and References
9 Procedure for Solving Eq. (6)
10 Additional Experiments Details and Results
11 Other Potential Applications
8 Proof of Theorem 2Before diving into the detailed proof, we present an outline of the structure of the proof and prove a lemma which we use in the proof of the theorem. Outline of the proof for the thereom
\ 1. Suppose we are given Vi and Vj , two test groups which satisfy the premise of the theorem;
\ 2. Then, we can approximate and bound the loss of each vertex in these groups based on the nearest vertex in the training set by extending the result from Theorem 1;
\ 3. If we can show that there exists a constant independent of the property of each test group, then we obtain the results of Theorem 2.
\

\

\
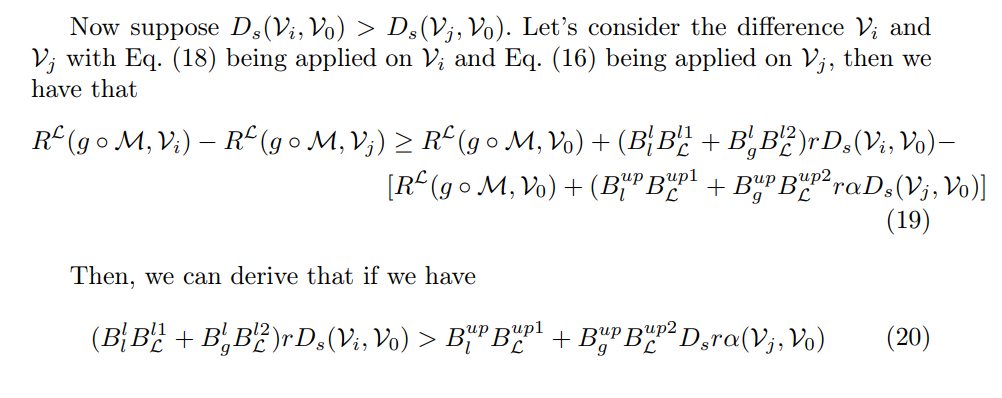
\
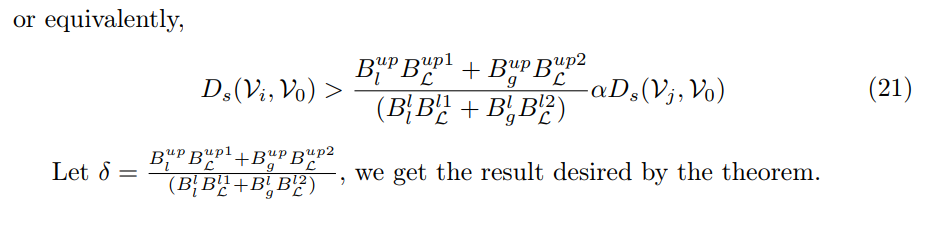
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright , Central Coast Communications, Inc.