Many computer vision and machine learning problems are modelled as learning tasks on graphs, where graph neural networks (GNNs) have emerged as a dominant tool for learning representations of graphstructured data. A key feature of GNNs is their use of graph structures as input, enabling them to exploit the graphs’ inherent topological properties—known as the topology awareness of GNNs. Despite the empirical successes of GNNs, the influence of topology awareness on generalization performance remains unexplored, particularly for node-level tasks that diverge from the assumption of data being independent and identically distributed (I.I.D.). The precise definition and characterization of the topology awareness of GNNs, especially concerning different topological features, are still unclear. This paper introduces a comprehensive framework to characterize the topology awareness of GNNs across any topological feature. Using this framework, we investigate the effects of topology awareness on GNN generalization performance. Contrary to the prevailing belief that enhancing the topology awareness of GNNs is always advantageous, our analysis reveals a critical insight: improving the topology awareness of GNNs may inadvertently lead to unfair generalization across structural groups, which might not be desired in some scenarios. Additionally, we conduct a case study using the intrinsic graph metric, the shortest-path distance, on various benchmark datasets. The empirical results of this case study confirm our theoretical insights. Moreover, we demonstrate the practical applicability of our framework by using it to tackle the cold start problem in graph active learning.

1 Introduction

Many problems in computer vision and machine learning are modeled as learning tasks on graphs. For example, in semantic segmentation, graphs model the relationships between different image regions, enhancing accuracy and context-aware segmentation. Graph neural networks (GNNs) have emerged as a dominant class of machine learning models specifically designed for learning representations of graph-structured data. They have demonstrated considerable success in addressing a wide range of graph-related problems in various domains such as chemistry [10], biology [37], social networking [6, 22], scene graph generation [46, 51] and visual relationship detection [24,43,49]. A defining characteristic of GNNs is their use of a spatial approach through message passing on the graph structure for feature aggregation. This enables GNNs to preserve structural information or dependencies (referred to as topology awareness) from the underlying graph structure, allowing them to be highly effective in tasks such as node classification. Fig. 1 illustrates the overall learning process of GNNs.

\ Despite their practicality and potential, there remains a lack of theoretical understanding about GNNs, particularly in the semi-supervised node classification setting where the dependencies among the data differ significantly from other machine learning models [25]. In this setting, the goal is to leverage relations, as captured by the graph structure, among the data and a small set of labelled nodes to predict labels for the remaining nodes. Most of the existing theoretical studies of GNNs have focused on the connection between the message-passing mechanism of GNNs and the Weisfeiler-Lehman isomorphism test [19], aiming to understand the ability of GNNs to differentiate different graph structures in the learned representations, known as the expressive power of GNNs. Inspired by the expressiveness studies, it is commonly believed that increasing topology awareness is universally beneficial and many studies focus on enabling GNNs to preserve more structural properties in the learned representation [29, 33, 48].

\ However, as GNNs become more reliant on and sensitive (aware) of graph structure as input, they may exhibit different generalization performances towards certain structural subgroups (distinct data subsets grouped by structural similarity to the training set) within the data. The quantification of GNN generalization across distinct structural subgroups is termed structural subgroup generalization [25]. Such considerations are vital in GNN application and development. For instance, within protein-protein interaction networks, these structural subgroups could represent different molecular complexes, influencing the accuracy of interaction predictions. Similarly, understanding how the topology awareness of GNNs influences generalization is essential when devising sampling strategies for training. The extent to which the generalization performance of GNNs is influenced by specific structural features of graph data is critical in deciding the composition of training datasets. Despite its importance, an understanding of the relationship between the topology awareness of GNNs and its structural subgroup generalization is still lacking. Furthermore, characterizing the topology awareness of GNNs poses a challenge, especially considering that different domains and tasks may prioritize distinct structural aspects. Therefore, a versatile framework is needed to assess the topology awareness of GNNs in relation to various structures.

\ To address this gap, in this paper, we propose a novel framework based on approximate metric embedding to study the relationship between structural subgroup generalization and topology awareness of GNNs in the context of semisupervised node classification. The proposed framework allows for the investigation of the structural subgroup generalization of GNNs with respect to different structural subgroups. More concretely, the main contributions of this work are summarized as follows.

\ 1. We propose a novel, structure-agnostic framework using approximate metric embedding to examine the interplay between GNNs’ structural subgroup generalization and topology awareness. This framework is versatile, accommodating various structural measures like shortest-path distance, and requires only the corresponding structural measure. Its simplicity in estimating key factors makes it applicable and generalizable to a wide range of scenarios.

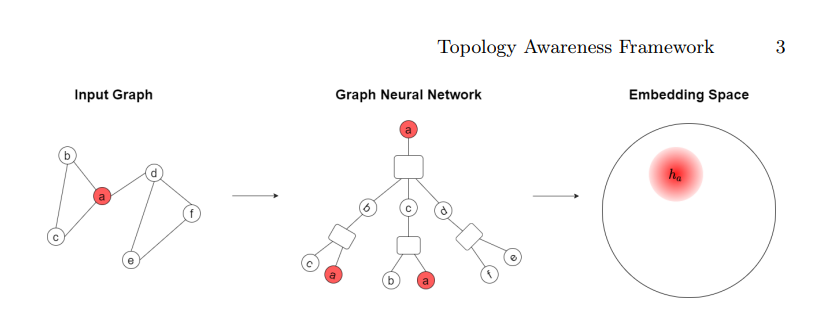
\ Fig. 1. An illustration of the learning process in a 2-layer GNN. The message-passing mechanism leverages the graph structure to aggregate information, thereby generating the representation/embedding ha for the target vertex a (highlighted in red).

\ 2. Through formal analysis within our framework, we establish a clear link between GNN topology awareness and their generalization performance (Theorem 1). We also demonstrate that while enhanced topology awareness boosts GNN expressiveness, it can result in uneven generalization performance, favouring subgroups more structurally similar to the training set (Theorem 2). Such structural property can be harmful (causing unfairness issues) or useful (informing design decisions) depending on the scenario. This challenges the prevailing belief that increased topology awareness universally benefits GNNs [29, 33, 48], emphasizing the importance of considering the relationship between topology awareness and generalization performance.

\ 3. We validate our framework through a case study on shortest-path distance, highlighting its practicality and relevance. The results corroborate our theoretical findings, showing that GNNs with heightened awareness of shortestpath distances excel in classifying vertex groups closer to the training set. Moreover, we demonstrate how our findings can be applied to mitigate the cold start problem in graph active learning [11,15], highlighting the practical implications of our framework and results.

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

Feed: Hacker Noon - Medium

View: Original article

Tags: application applications framework small social underlying