and the distribution of digital products.
DM Television
Understanding GAN Mode Collapse: Causes and Solutions
\ Generative Adversarial Networks (GANs) are a type of deep learning model that has gained a lot of attention in recent years due to their ability to generate realistic images, videos, and other types of data. GANs consist of two neural networks, a generator, and a discriminator, that play a two-player game. The generator produces synthetic data, while the discriminator tries to distinguish between real and fake data. The generator is trained to produce output that can fool the discriminator, while the discriminator is trained to correctly distinguish between real and fake data. Despite their success, GANs are not without their challenges. One of the most significant challenges is mode collapse.
\ Mode collapse occurs when a GAN generates only a limited set of output examples instead of exploring the entire distribution of the training data. In other words, the generator of the GAN becomes stuck in a particular mode or pattern, failing to generate diverse outputs that cover the entire range of the data. This can result in the generated output appearing repetitive, lacking in variety and detail, and sometimes even being completely unrelated to the training data.
\ In this paper, I explain the causes of mode collapse in GANs. There are several reasons why mode collapse can occur in GANs. One cause is catastrophic forgetting, where knowledge learned in a previous task is destroyed by learning in a current task. Another cause of mode collapse is discriminator overfitting, which results in the generator loss vanishing. In the next two sections, I will provide an explanation of these two behaviors.
\
Catastrophic forgettingCatastrophic forgetting refers to the phenomenon in which a model trained on a specific task forgets the knowledge it has gained while learning a new task. Let’s examine a GAN consisting of a generator G and a discriminator D. During the t-th training step; the generator produces samples with distribution pG that approximates the true data distribution pR. At each training step, the discriminator is trained to differentiate between the real data pR and the generated samples pG. However, as p_G shifts with each step, the discriminator must adapt to new classification tasks.
\ Let’s analyze catastrophic forgetting by training a GAN on simple synthetic 2D data. The dataset consists of six Gaussian distributions arranged in a circle, as shown in Figure 1. The blue datapoints represent the real data, while the orange datapoints represent the generated samples. The model’s task is to replicate the distribution of the blue datapoints. The arrows indicate the direction of decreasing generator loss (-d(Loss_G) / dx). As the generator loss decreases, the discriminator output D(x) increases. Therefore, we can interpret the arrows as indicating the direction of increasing confidence of the discriminator in identifying true datapoints. It’s worth noting that the discriminator’s score increases when you move along the arrows in proportion to the length of the arrow.
\
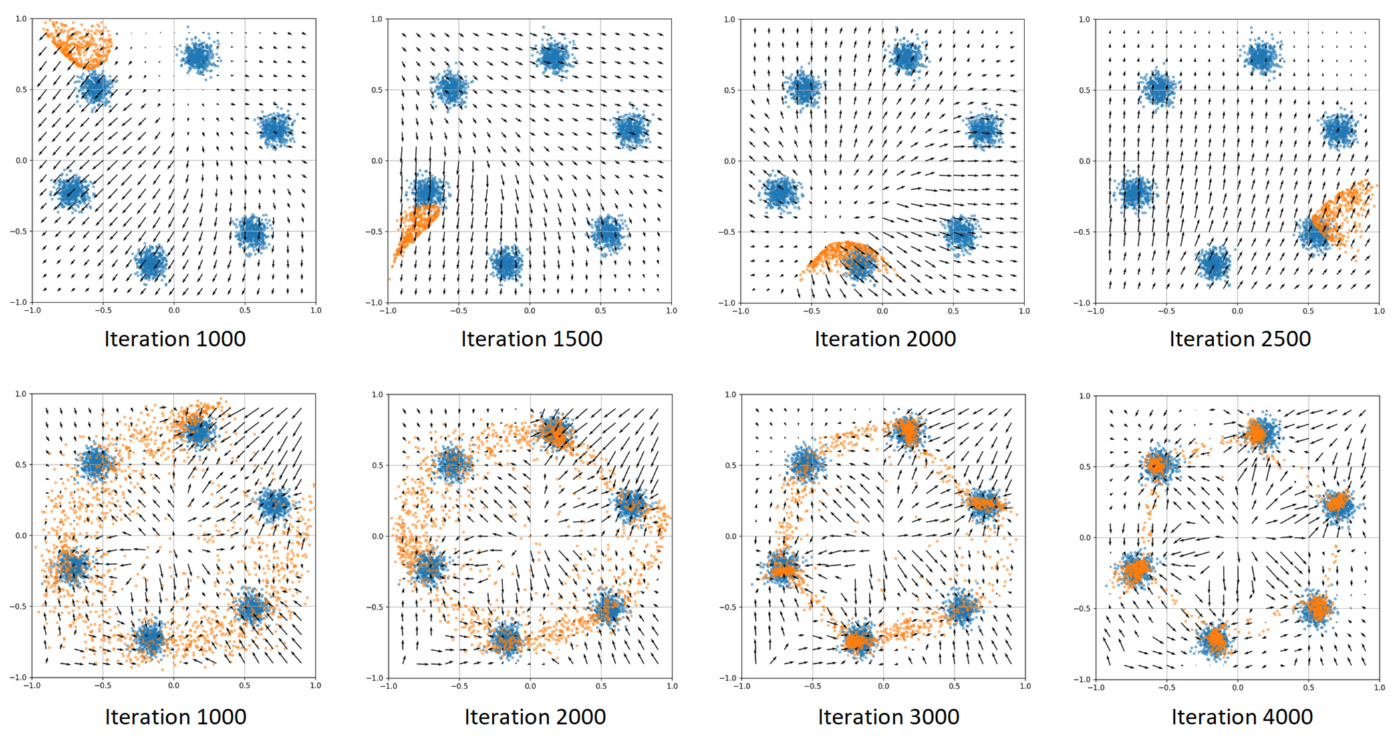
\ Looking at the behavior of the discriminator depicted at the top of Figure 1, it becomes apparent that it gives higher scores to points that are further from the generated samples, and it pays no attention to real datapoints. This happens because the generated samples are located in a small region, and consequently, it becomes easy to distinguish between the true and generated distributions by simply giving low scores to the generated samples and high scores to other regions. Additionally, due to the monotonic nature of the gradients around the generated data points, they are unable to spread across different areas. Another observation is that the direction of the gradients can be opposite to itself at different iterations and depend only on the generated samples. This implies that the model forgets the knowledge gained from previous steps, leading to catastrophic forgetting. Training behavior without mode collapse is demonstrated at the bottom of Figure 1. The discernible pattern is that, at GAN convergence, real datapoints are the local maxima of the discriminator.
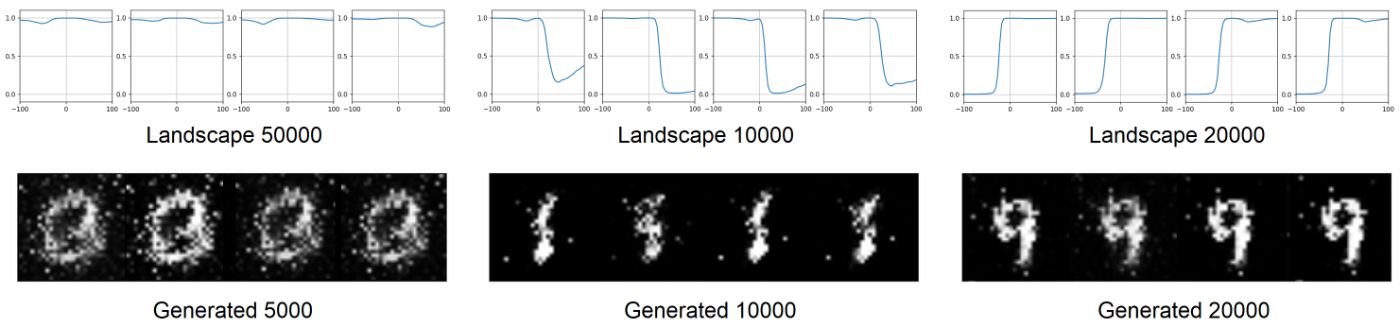
\ To determine whether catastrophic forgetting occurs in actual multivariate data, let’s visualize the surface of the discriminator that was trained on the MNIST dataset. As the distribution of images in the dataset is multidimensional, it is not possible to visualize it in 2D. However, we can take a random line through the image and observe how the score of the discriminator changes along the line. We will visualize the value of f(x) = D(x + k*u), where u is a random directional vector and k is a shift factor. Figure 2 shows the plot of function f. Moreover, it illustrates that the generator produces similar outputs, indicating a mode collapse, and the discriminator scores for the same images change between training steps. Thus, GANs display the same catastrophic forgetting tendencies as they do when trained on symmetric 2D datasets.
\
\
Discriminator overfittingI applied the same visualization method to the GAN that did not suffer from mode collapse and demonstrated diverse and fidelity outputs, as shown in Figure 3. During GAN training, the function f(k) consistently exhibits a local maximum at k=0 for every real datapoint. This suggests that the discriminator is exposed to local maxima on real datapoints. When a generated sample falls within the basin of attraction of a real datapoint, applying gradient updates directly to the generated sample will move it toward the real datapoint. The existence of distinct attractors (local maxima) in various regions of the data space moves different generated samples in different directions, distributing them throughout the space and effectively minimizing mode collapse.
\

\ Figure 4 displays GAN outputs with mode collapse, which is caused by discriminator overfitting. The maxima depicted in Figure 4 are significantly sharper than those in Figure 3 due to discriminator overfitting on the real datapoints, causing the scores of nearby datapoints to approach zero. This results in the emergence of numerous flat regions, where the discriminator’s gradients towards the datapoints in those regions are vanishingly small. As a result, the generated samples residing in a flat region cannot move toward the real datapoints due to the vanishing gradient. Thus, the real datapoints depicted in Figure 4 have limited basins of attraction and are unable to efficiently distribute generated samples throughout the space. Consequently, the diversity of the generated samples decreases, leading to mode collapse. To prevent this, the local maxima must have a wide shape, indicating a large basin of attraction that pulls generated samples towards different directions.
\

\ In conclusion, Generative Adversarial Networks (GANs) are powerful deep learning models that are widely used for generating realistic data. In this article, we have explored two causes of mode collapse in GANs: catastrophic forgetting and discriminator overfitting. By understanding the causes of mode collapse, we can better develop GANs that are capable of generating diverse and high-quality outputs.
\ Thank you for reading this article. I hope that it provided some value and insight for you.
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright , Central Coast Communications, Inc.