and the distribution of digital products.
Theory Coherent Shrinkage of Time Varying Parameters in VARs: A Appendix
:::info Andrea Renzetti, Department of Economics, Alma Mater Studiorium Universit`a di Bologna, Piazza Scaravilli 2, 40126 Bologna, Italy.
:::
Table of LinksForecasting with the TC-TVP-VAR
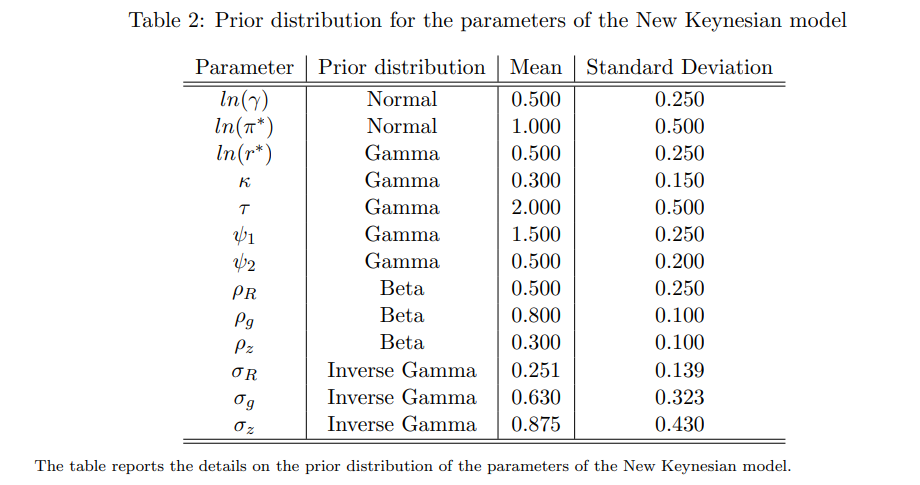
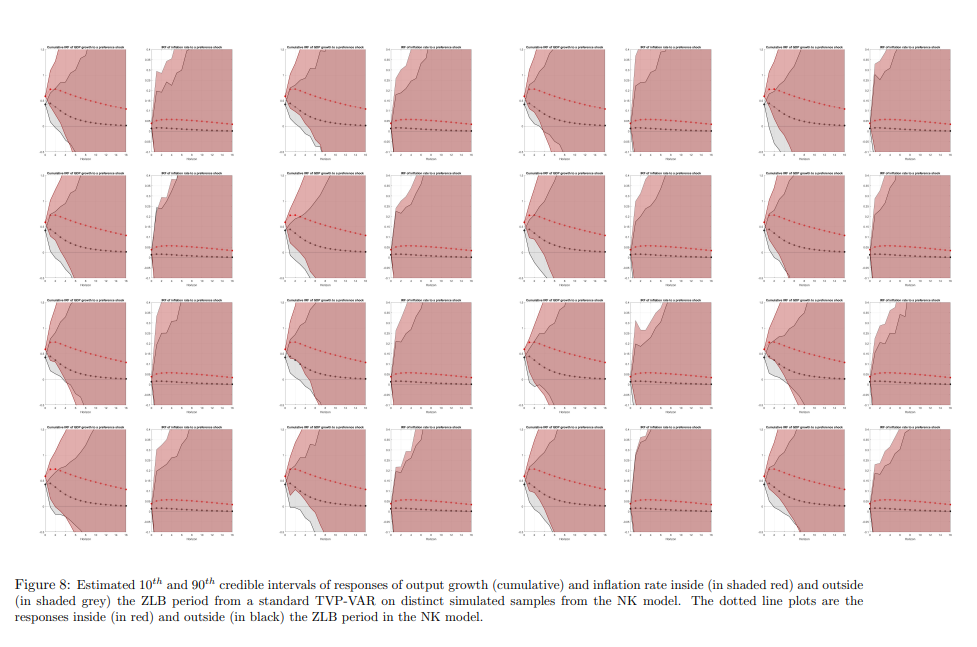
Response analysis at the ZLB with the TC-TVP-VAR
A Appendix A.1 Theory Coherent TVP-VAR A.1.1 Time Varying Parameters by dummy observationsStarting from:
\
\ we can write the TVP-VAR in static compact form as:
\
\ Suppose we want to specify independent RW stochastic processes for all the coefficients in Φ as:
\
\ This is just another way of writing:
\
The integrating constant of the Normal-Inverse-Wishart prior
\
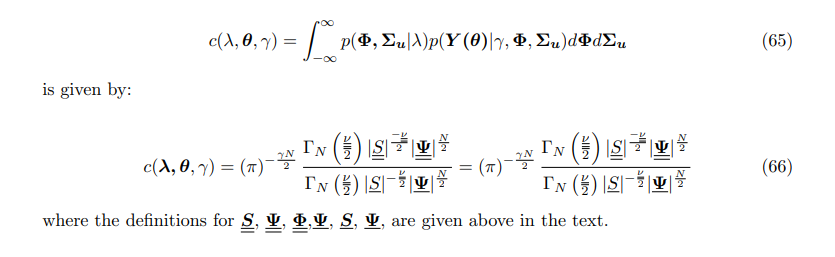
\ Considering the three first blocks we get
\
The marginal likelihood is given by:
\
Following the same steps as in (Giannone et al. 2015) it can be re-written as :
\
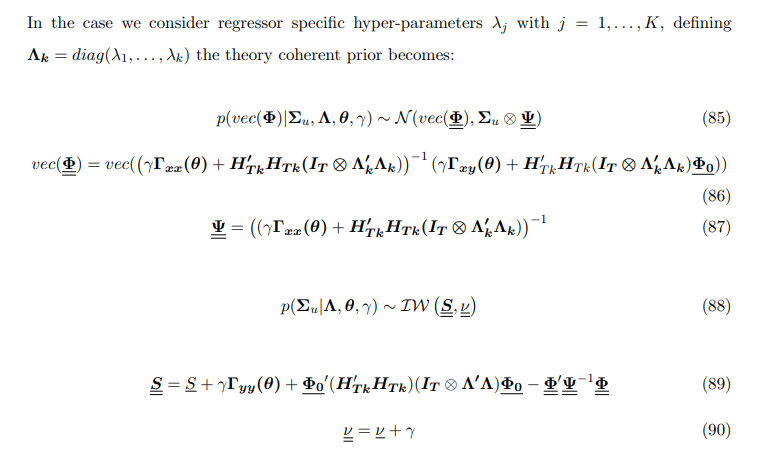
The competing models in the out of sample forecasting exercise in Section 3 are
\ • A constant parameters VAR with flat prior.
\ • A constant parameters VAR with Normal Inverse-Wishart prior.
\ • A TVP-VAR model
\ The VAR with Normal Inverse-Wishart prior is given by:
\
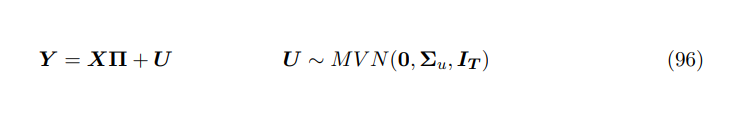
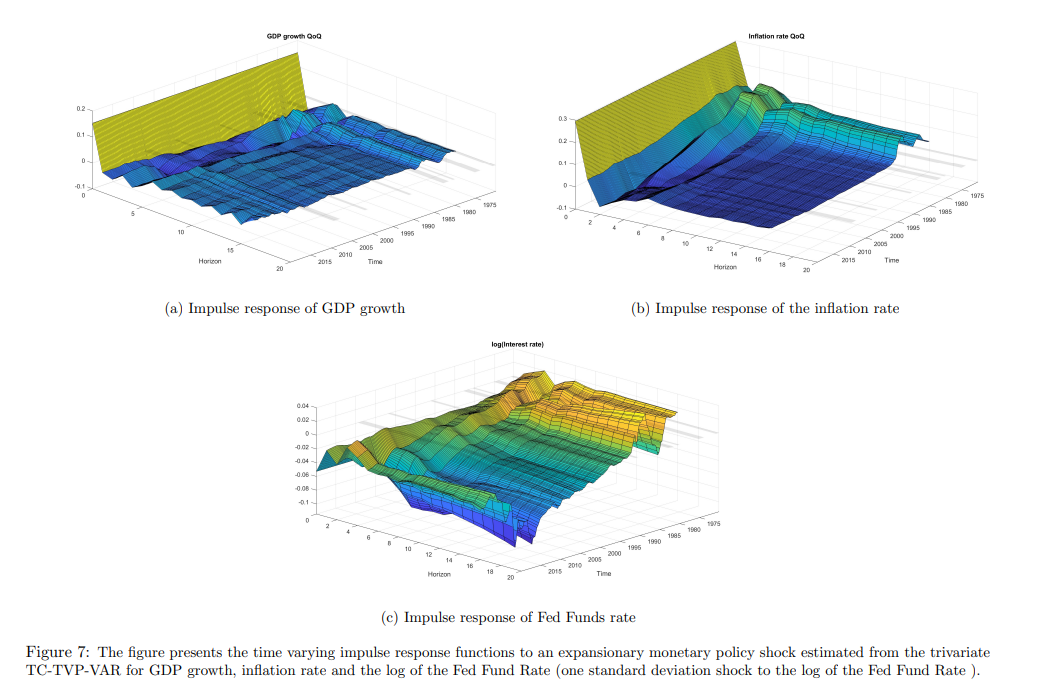
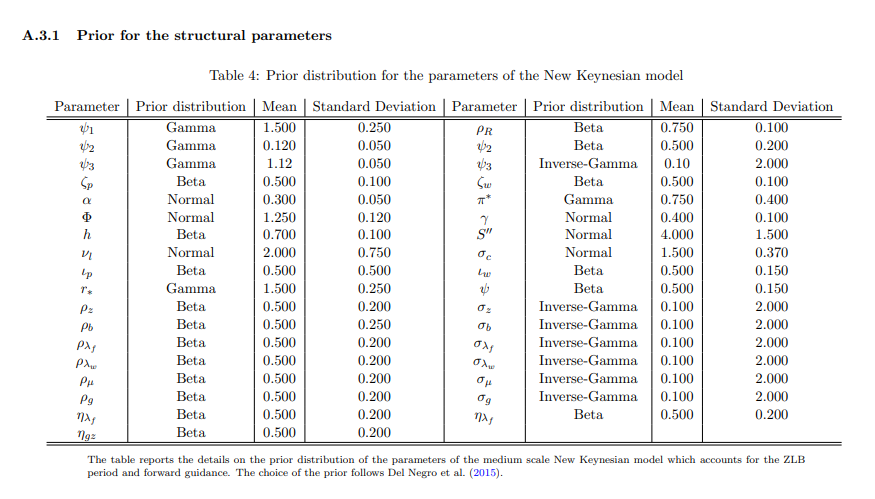
The model is taken from Del Negro et al. (2015) and it is a version of the popular medium scale New Keynesian model in Smets et al. (2007). The set of log-linearized equilibrium conditions of the model is
\
\
\
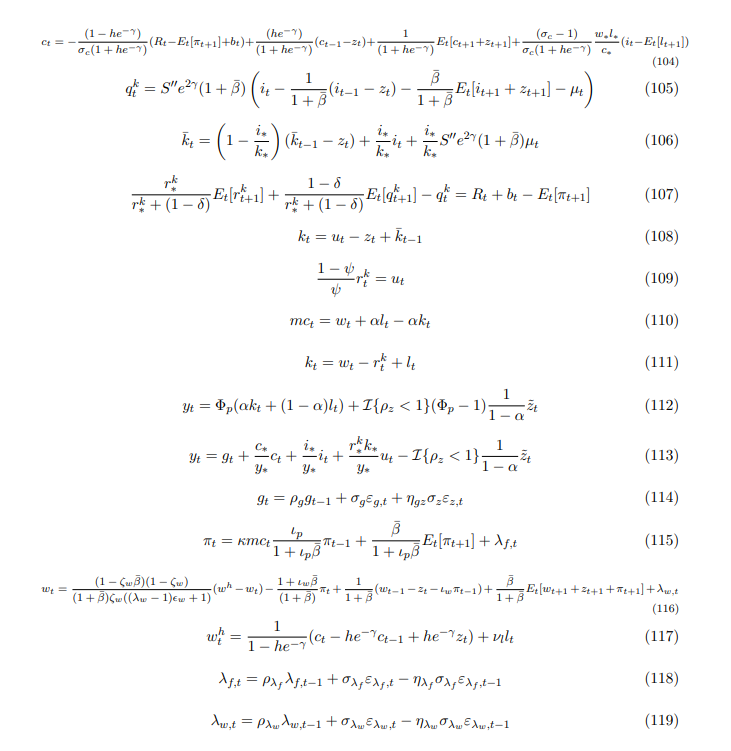
:::info This paper is available on arxiv under CC 4.0 license.
:::
\
