Teaching AI to Know When It Doesn’t Know

:::info Authors:

(1) Anonymous authors Paper under double-blind review Jarrod Haas, SARlab, Department of Engineering Science Simon Fraser University; Digitalist Group Canada and [email protected];

(2) William Yolland, MetaOptima and [email protected];

(3) Bernhard Rabus, SARlab, Department of Engineering Science, Simon Fraser University and bernhardt[email protected].

:::

\

• Abstract and 1 Introduction
• 2 Background
• 2.1 Problem Definition
• 2.2 Related Work
• 2.3 Deep Deterministic Uncertainty
• 2.4 L2 Normalization of Feature Space and Neural Collapse
• 3 Methodology
• 3.1 Models and Loss Functions
• 3.2 Measuring Neural Collapse
• 4 Experiments
• 4.1 Faster and More Robust OoD Results
• 4.2 Linking Neural Collapse with OoD Detection
• 5 Conclusion and Future Work, and References
• A Appendix
• A.1 Training Details
• A.2 Effect of L2 Normalization on Softmax Scores for OoD Detection
• A.3 Fitting GMMs on Logit Space
• A.4 Overtraining with L2 Normalization
• A.5 Neural Collapse Measurements for NC Loss Intervention
• A.6 Additional Figures

2 Background 2.1 Problem Definition

\ To evaluate models, we merge ID and OoD images into a single test set. OoD performance is then a binary classification task, where we measure how well OoD images can be separated from ID images using a score derived from our model. Our scoring rule is derived from a Gaussian Mixture Model (GMM) fit over z (as discussed below) rather than the softmax outputs used for classification. We retain softmax outputs as we want to make sure that our ability to distinguish ID and OoD images does not hinder our ability to classify ID images.

2.2 Related Work

Until recently, most research toward uncertainty estimation in deep learning took a Bayesian approach. The high number of parameters in DL models renders posterior integration intractable, so approximations (typically variational inference) have been used (Gal and Ghahramani, 2016). Monte Carlo Dropout (MCD), which draws a connection between test time dropout and variational inference, has emerged as a popular method to estimate uncertainty (Gal and Ghahramani, 2016). Despite MCD’s simplicity, scalability and applicability to nearly any model architecture, it is often outperformed by deterministic ensembles (Ovadia et al., 2019). Lakshminarayanan et al. observed that a simple average over the predictions of multiple deterministic models with the same architecture but starting from unique parameter initialisations produces a competitive uncertainty estimate (Lakshminarayanan et al., 2017).

\ The extra compute required for running multiple model passes at test time and for training and testing ensembles has motivated recent research around single model, single pass uncertainty estimates. Van Amersfoort et al. enforce a bi-Lipschitz penalty on gradients during training to create a distance-aware feature space in their Deep Uncertainty Quantification method (DUQ), which is then measured with a radial basis function (RBF) instead of a standard linear classifier (Van Amersfoort et al., 2020). While showing some promise, bi-lipschitz loss penalties can be unstable during training (Mukhoti et al., 2021). In later work, van Amersfoort et al. (2021) replace the RBF apparatus with a deep kernel and a point Gaussian Process (GP), while maintaining distance-awareness in feature space by adding spectral normalization throughout the model. A similar approach by Liu et al. (2020) uses a Random Fourier Feature approximation to construct the GP (called Spectral-normalized Neural Gaussian Process, or SNGP), but results are not as competitive. Lee et al. (2018) propose fitting a class-wise conditional Gaussian with shared covariance matrix to multiple layers, but employ OoD and adversarial data to learn a weighted average of scores over layers. They also add noise to inputs at test time to enhance OoD separability. ODIN produces competitive results, but also requires OoD data for hyperparameter tuning (Liang et al., 2017). Generalized ODIN relaxes this requirement (Hsu et al., 2020), but both versions require an additional backward pass at test time to perturb inputs. Finally, Hendrycks and Gimpel (2016) proposed simply measuring maximum softmax scores of converged models as a benchmark for OoD detection. We believe that OoD detection has moved well past what out-of-the-box, uncalibrated softmax scores can accomplish, and that Deep Deterministic Uncertainty provides a better benchmark for the evaluation of single pass methods (Mukhoti et al., 2021).

2.3 Deep Deterministic Uncertainty

\ \

\ Mukhoti et al.’s approach is motivated by a simple idea: feature space must be "well regularized", i.e. images that are very different in input space are different in feature space ("sensitivity"), and images that are similar in input space are similar in feature space ("smoothness"). This can be interpreted as enforcing a bi-Lipschitz constraint over feature space:

\

\ Under a well-regularized feature space arising from a converged model, OoD images should be mapped less often to ID feature space. OoD detection is then a matter of measuring the distance of an extracted feature fθ(x) from dense, class-wise feature-space clusters that emerge during training. Additionally, fitting a GMM over these clusters prevents the network from assigning high confidence to points far away from the class clusters simply because they fall within a decision region (Figure 1).

\ Importantly, if a feature extractor is too sensitive, ID feature vectors may not cluster tightly enough, and ID images would then get flagged as OoD due to their distance from modes in the GMM. If too smooth, the feature extractor won’t pick up on differences between OoD and ID images, and may place OoD images too close to GMM modes.

\ Our ablation study results (Table 2) show that L2 normalization over feature space improves OoD detection when used in addition to the bi-Lipshitz-enforcing regularization techniques proposed in the DDU benchmark. In Section 4, we show an empirical link between L2 normalization, Neural Collapse and OoD detection performance.

2.4 L2 Normalization of Feature Space and Neural Collapse

DDU works well under the assumption of a well-regularized feature space. However, the bi-Lipschitz continuity encouraged by the aforementioned methods affords no explicit structure over feature space. We suggest that the simplex ETF structure arising from Neural Collapse improves sensitivity and smoothness and is thereby linked with better OoD detection results.

\

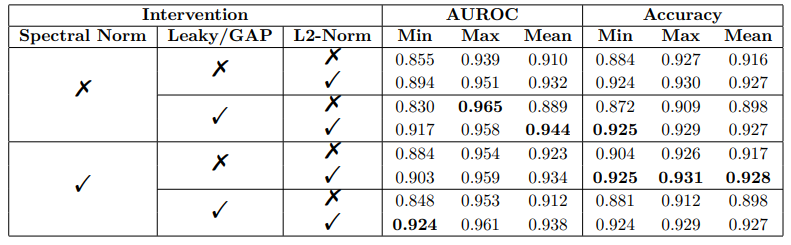
\ Although feature space is structured once model accuracy converges–this being a simple consequence of the decision layer’s need to divide feature space in order to produce class predictions–the structure that emerges is limited and highly variable, even under bi-Lipschitz regularization techniques: class clusters have high nonuniform variance, and clusters are only separated to the degree that the decision layer can satisfy training demands for low cross-entropy loss (Figure 8). As a consequence, it is well known that data embedded far from class clusters can have high confidence scores (Hein et al. (2018), Figure 1). This is also evidenced by models with high accuracy and high-variance class clusters (Table 2, 3).

\ Given that we want to organize feature space in the manner most conducive to OoD detection, we suggest that following the principles of sensitivity and smoothness should be the aim: tightening clusters and placing them away from each other. Features in this proposed configuration would have low within-class variance (smoothness), and higher between-class variance (sensitivity). Intuitively, networks trained to adhere to this structure should excel at mapping known inputs to within these tight clusters, while unknown inputs should become difficult to map precisely and would tend to fall outside of the clusters and into the empty feature space around them.

\ Although there are many possible ways to structure feature space, a reasonable starting point is a hypersphere. Numerous works exist that seek to exploit the properties of hyperspheres in order to make high-dimensional information-comparison problems, like OoD detection, more tractable (Sablayrolles et al., 2018; Zhou et al., 2020; Zheng et al., 2022; Liu et al., 2017). An interesting property of a hypersphere on RD is that if D is sufficiently larger than the number of points N that one wishes to embed on its surface, the maximum distance between all points is obtained when all point-wise distances are equal. In other words, constraining feature space to a hypersphere allows a structure over which class clusters could be maximally and equally distanced from one another, providing substantial unused space between clusters. We note that fully maximizing between-class distance is probably not ideal, as this would rigidly enforce too much sensitivity i.e. we would like the feature extractor to have some flexibility in placing more similar classes closer together. A balance must be struck between spreading classes out and respecting appropriate Lipschitz bounds.

\ Papyan et al. (2020) recently observed a phenomenon known as Neural Collapse (NC) which progresses as networks are trained, ultimately leading to feature space and decision space conforming to a structure known as a simplex equiangular tight-frame (see Section 3.2 for definition and measurement). One of the key properties of NC is variability collapse, wherein class clusters in embedding space collapse toward a single point in feature space. Additionally, as feature space convergences to a simplex ETF, clusters are positioned at maximally equiangular distances from each other. In other words, DNNs gradually and automatically proceed toward the hypersphere structure we seek (Figure 2).

\

\ The difficulty here is that NC fully converges only after the terminal phase of training, i.e. after crossentropy loss goes to zero. This means that networks need to be substantially over-trained before feature space becomes structured in a manner which we can fully exploit.

\ Since the Simplex ETF structure also results in class clusters existing on the surface of a hypersphere (a consequence of equinormality, see Section 3.2), we hypothesize that it is possible to induce NC more quickly by simply constraining feature space to a hypersphere from the onset of training. L2 normalization over feature space constrains feature vectors to a point on the surface of a hypersphere by restricting the magnitude of all feature vectors to be uniform:

\

\

:::info This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.

:::

\