and the distribution of digital products.
Simulation Model for DAG-PROTOCOL Under Incentive Attacks
IX. Discussion and Future Work
VI. SIMULATION MODELWe created a simulation model to conduct various experiments investigating the behavior of DAG-PROTOCOL under incentive attacks related to the problems identified in Sec. III and thus Hypothesis 1. Some experiments were designed to provide empirical evidence for the conclusions from Sec. V.
\ A. Abstraction of DAG-PROTOCOL
\ For evaluation purposes, we simulated the DAGPROTOCOL (with RTS) by modeling the following aspects:
\ • All blocks in DAG are deterministically ordered.
\ • The mining rewards consist of transaction fees only.
\ • A fee of a particular transaction is awarded only to a miner of the block that includes the transaction as the first one in the sequence of totally ordered blocks.
\ Also, in terms of PHANTOM/GHOSTDAG terminology, we generalize and do not reduce transaction fees concerning the delay from “appearing” of the block until it is strongly connected to the DAG. Hence, we utilize γ = 1. In other words, for each block A, the discount function does not penalize a block according to its gap parameter c(A), i.e. γ(c(A)) = 1. Such a setting is optimistic for honest miners and maximizes their profits from transaction fees when following the RTS strategy. This abstraction enables us to model the concerned problems of considered DAG-PROTOCOLS (see Sec. IV).
\ B. (Simple) Network Topology
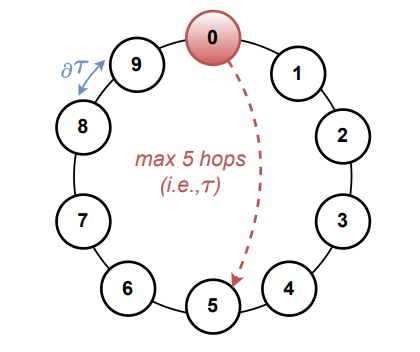
\ We created a simple network topology that is convenient for proof-of-concept simulations and encompasses some important aspects of the real-world blockchain network. In particular, we were interested in emulating the network propagation delay τ to be similar to in Bitcoin (i.e., ∼ 5s at most of the time in 2022), but using a small ring topology. To create such a topology, we assumed that the Bitcoin network contains 7592 nodes, according to the snapshot of reachable Bitcoin nodes found on May 24, 2022.[11] In Bitcoin core, the default value of the consensus node’s peers is set to 8 (i.e., the node degree).[12] Therefore, the maximum number of hops that a gossiped message requires to reach all consensus nodes in the network is ∼ 4.29 (i.e., log8(7592)). Moreover, if we were to assume 2 − 3x more independent blockchain clients (that are not consensus nodes), then this number would be increased to 4.83–4.96. To model this environment, we used the ring network topology with 10 consensus nodes (see Fig. 4), which sets the maximum value of hops required to propagate a message to 5. Next, we set the inter-node propagation delay ∂τ to 1s, which fits assumed τ (i.e., 5s / 5 hops = 1s). Later, we will create more complex network topology (see Sec. VII-E).
\
\ C. Simulator
\ There are many simulators [36] that model blockchain protocols, mainly focusing on network delays, different consensus protocols, and behaviors of specific attacks (e.g., SimBlock [4], Blocksim [1], Bitcoin-Simulator [17], etc.). However, none of these simulators was sufficient for our purposes due to missing support for multiple chains (or their abstraction) and incentive schemes assumed in DAG-PROTOCOLS. To verify Hypothesis 1, we built a simulator that focuses on the mentioned problems of DAG-PROTOCOLS. In detail, we started with the Bitcoin mining simulator [14], which is a discrete event simulator for the PoW mining on a single chain, enabling a simulation of network propagation delay within a specified network topology.
\ We extended this simulator to support DAG-PROTOCOLs, enabling us to monitor transaction duplicity, throughput, and relative profits of miners with regard to their mining power. The simulator is written in C++. The implementation utilizes the Boost library [7] for better performance and the special structures for simulation, such as the multi-index mempool [22], enabling effective management of the mempool in the case of any transaction selection strategy.[13]
\ In addition, we added more simulation complexity to simulate each block, including the particular transactions (as opposed to simulating only the number of transactions in a block [14]). Most importantly, we implemented two different transaction selection strategies – greedy and random. For demonstration purposes, we implemented the exponential distribution of transaction fees in mempool, based on several graph cuts of fee distributions in mempool of Bitcoin from [20].[14] Our simulator is available at https://www.dropbox. com/s/vqpgqqy01qh1pcv/.
\
:::info Authors:
(1) Martin Peresıni, Brno University of Technology, Faculty of Information Technology ([email protected]);
(2) Ivan Homoliak, Brno University of Technology, Faculty of Information Technology ([email protected]);
(3) Federico Matteo Bencic, University of Zagreb, Faculty of Electrical Engineering and Computing ([email protected]);
(4) Martin Hruby, Brno University of Technology, Faculty of Information Technology ([email protected]);
(5) Kamil Malinka, Brno University of Technology, Faculty of Information Technology ([email protected]).
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
https://bitnodes.io/nodes/
\
Nevertheless, the node degree is often higher than 8 in reality [32].
\
Greedy transaction strategy requires a mempool with transactions ordered by fees, while RTS strategy requires the hash-map data structure. Therefore, it is challenging to efficiently utilize them at the same time.
\
Distribution of transaction fees in mempool might change over time; however, it mostly preserves the low number of high-fee transactions in contrast to the higher number of low-fee transactions, which is common with the exponential distribution.
\