Proving Theorems for Rust’s Dancing Links in ACL2

:::info Author:

(1) David S. Hardin, Cedar Rapids, IA USA ([email protected]).

:::

1 Introduction

2 Dancing Links

3 The Rust Programming Language

4 RAC: Hardware/Software Co-Assurance at Scale

5 Rust and RAR

5.1 Restricted Algorithmic Rust

6 Dancing Links in Rust and 6.1 Definitions

6.2 Translation to ACL2

6.3 Dancing Links Theorems

7 Related Work

8 Conclusion

9 Acknowledgments and References

\

Once we have translated the circular doubly-linked list functions into ACL2, we can begin to prove theorems about the data structure implementation. We begin by defining a “well-formedness” predicate for CDLLs.

\

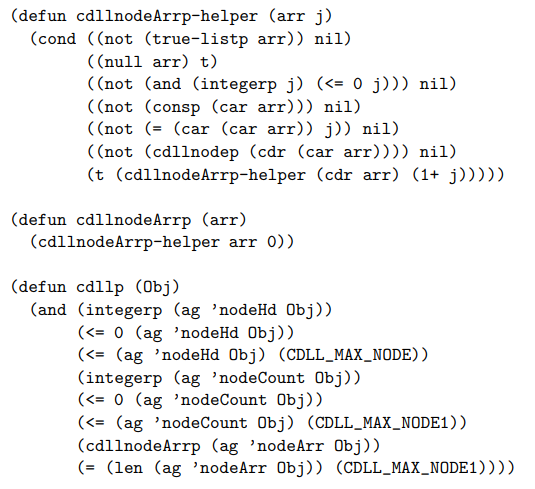
\ Given this definition of a good CDLL state, we can prove functional correctness theorems for Dancing Links operations, of the sort stated below. Note that this proof requires some detailed well-formedness hypotheses related to the prev and next indices for the nth element:

\

\ ACL2 performs the correctness proof for this cdllrestore of cdllremove theorem automatically. In addition to the Dancing Links operator proofs, we have proved approximately 160 theorems related to the CDLL data structure, including theorems about cdllcns() (cons equivalent), cdll- rst() (cdr equivalent), cdllsnc() (add to end of data structure), cdlltsr() (delete from end of data structure), cdll_nth(), etc. All of these proofs will be made publicly available in the ACL2 workshop books repository.

\

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\