Polar Coordinates for Accurate Iso-Distance Curve Alignment in Vehicle Simulations

:::info Authors:

(1) Mehdi Naderi;

(2) Markos Papageorgiou;

(3) Dimitrios Troullinos;

(4) Iasson Karafyllis;

(5) Ioannis Papamichail.

:::

Abstract and Introduction

Vehicle Modeling

The Nonlinear Feedback Control

OD Corridors and Desired Orientations

Boundary and Safety Controllers

Simulation Results

Conclusion

Appendix A: Collision Detection

Appendix B: Transformed ISO-Distance curves

Appendix C: Local Density

Appendix D: Safety Controller Details

Appendix E: Controller Parameters

References

For the iso-distance curve transformation to align with the desired orientation, new polar coordinates are defined whose origin is found by crossing two lines perpendicular to the vehicles’ rear axles, while having the ego vehicle’s desired deviation from the circular angle. This implies that the coordinates are different for each pair of vehicles. The lines’ equations, according to Fig. 20, can be written as

\

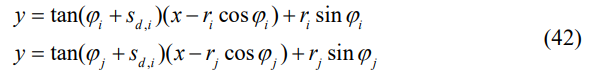
\ Note that each vehicle projects other vehicles on its own coordinates; therefore, in both equations of (42), the desired orientation of vehicle i is taken into account. Intersecting above

\

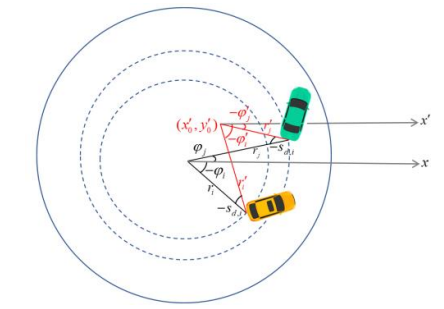
\ equations gives the centre of new coordinates as

\

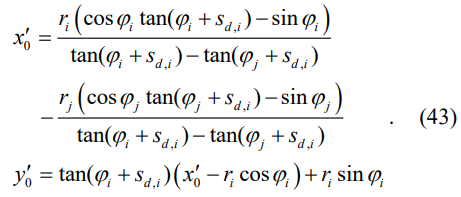
\ Then, the radius and angle of each vehicle in the new coordinates is calculated by

\

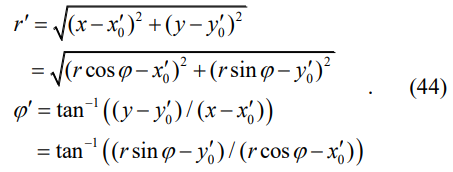
\ Furthermore, the distance in the new coordinates is

\

\

:::info This paper is available on arxiv under CC 4.0 license.

:::

\