and the distribution of digital products.
Neutrality, Trade-Offs, and the Future of Inflation Models
:::info Author:
(1) David Staines.
:::
Table of Links4 Calvo Framework and 4.1 Household’s Problem
4.3 Household Equilibrium Conditions
4.5 Nominal Equilibrium Conditions
4.6 Real Equilibrium Conditions and 4.7 Shocks
5.2 Persistence and Policy Puzzles
6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems
7 General Linearized Phillips Curve
8 Existence Results and 8.1 Main Results
9.2 Algebraic Aspects (I) Singularities and Covers
9.3 Algebraic Aspects (II) Homology
9.4 Algebraic Aspects (III) Schemes
9.5 Wider Economic Interpretations
10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs
10.4 Microeconomic Interpretation
\ Appendices
A Proof of Theorem 2 and A.1 Proof of Part (i)
B Proofs from Section 4 and B.1 Individual Product Demand (4.2)
B.2 Flexible Price Equilibrium and ZINSS (4.4)
B.4 Cost Minimization (4.6) and (10.4)
C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence
D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium
D.2 Profits and Long-Run Growth
E Slopes and Eigenvalues and E.1 Slope Coefficients
E.4 Rouche’s Theorem Conditions
F Abstract Algebra and F.1 Homology Groups
F.4 Marginal Costs and Inflation
G Further Keynesian Models and G.1 Taylor Pricing
G.3 Unconventional Policy Settings
H Empirical Robustness and H.1 Parameter Selection
I Additional Evidence and I.1 Other Structural Parameters
I.3 Trend Inflation Volatility
10.3 Coefficient PropertiesThis subsection considers the salient properties of the slope coefficients, with particular emphasis on the output. There are surprising connections with historical debates in macroeconomics and alternative models of price rigidity. The other coefficients embody subtle trade-offs or overturn existing intuition. The properties of the error structure deserve a comprehensive treatment elsewhere.
10.3.1 Output NeutralityAt the outset I confirm that the output coefficient from Section 7 is strictly less than with the singular Phillips curve back in Section 5.
\
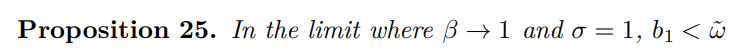
\ Proof. The proof is accomplished with the following decomposition
\
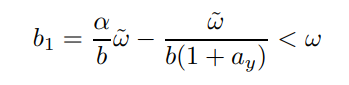
\ the strict inequality arises because the underlying coefficients are all positive and b > α.
\ This is likely to improve the fit to the data, as the slope is typically too large in the positive direction. The crucial difference is that the slope need not be positive, in fact it inherits its sign from the term α(1 + ay) − 1.
\ The classical dichotomy indicates the efficient value is zero. In fact, the term represents two competing inter-temporal distortions. α < 1 represents the discounting term in the price setting problem, additional to β, which we have taken towards unity. The lesson is that the uncertain prospect of re-optimization causes firms to overweight the present relative to the future in their pricing decision. This should give rise to staggered nominal adjustment in response to any shock. The theme if not the specific argument should be familiar to macroeconomists
\ On the other hand, the output response may be more surprising. When firms engage in staggered optimization it creates inter-temporal substitution motives. Therefore, anything that impacts financial conditions will directly influence pricing decisions. The central bank by committing to adjust monetary policy in response to shocks will effect how firms adjust to those shocks. This justifies the policy invariance aspect of Lucas’ critique, whilst overturning the observational equivalence idea because these forces are missing from the classical model. The result is robust to a battery of real frictions that rescale ˜ω by 1/(1+ R).[95] This suggests that nominal rather than supply side factors determine the fundamental shape of the Phillips curve.
\ Output neutrality plays into an old debate in macroeconomics featuring the Keynesian, Austrian and Classical schools. Snowdon and Vane [2005] is a suitable background source. The Austrian school, such as von Hayek [2012], emphasised that active monetary policy would distort inter-temporal production and investment decisions. It is unlikely that pricing was the foremost mechanism in their analysis.[96] Nevertheless, it is important to confirm that this mechanism is a priori plausible and obviously should be investigated, in models with more complicated production and financial sectors. Mainstream economists argued correctly, that this was not possible, unless there were alternative sources of market failure. Keynesian economics at the time was not able to supply this but now this is possible. It should be achievable to supply objective content to this type of debate, even if not everyone will be convinced. With the credible prospect of two market failures cancelling out, this is a clear example of the theory of second best (Lipsey and Lancaster [1956]), a mainstay of welfare analysis.
\ Many will be surprised or even concerned about a Phillips curve without a positive feedback from output onto inflation. This is not necessarily a problem. The cursory analysis of Section 3 indicates my flat Phillips curve is a better fit than its very steep counterpart. It is an opportunity rather than a threat when a micro-founded solution fails to conform to a popular conjecture. There may be other frictions that favor a positive slope. The goal is a suite of models containing a plethora of well-understood dynamic market failures, that combined give a powerful insight into typical business cycle dynamics.
\ A particular case of interest is where ay = 0 and the limit where α → 1. This can be viewed as the case where time periods become arbitrarily short, holding constant the overall frequency of adjustment.[97] Discounting distortions are absent, as opposed to just cancelling out. This effects how inflation is determined. It is a simple average of its past and (expected) present value. This agrees with the Taylor [1979] model of staggered contracts, where every price is reset after a fixed time horizon. In particular, this pattern corresponds to the simplest possible form with contract lasting two periods. A feature specific to Calvo is that as the reset rate per period declines away the structural error terms vanish so an additional error et, such as the unfortunate mark-ups shocks would have to be added to make the Phillips curve identified.
\ In fact output neutrality can be extended to Taylor pricing and may be universal across staggered optimization models. To see how consider the accelerationist Phillips curve
\
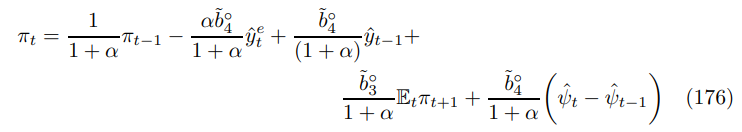
\ in the limit where α → 1. The coefficients on output and its lag are of common magnitude but opposite sign. I demonstrate in Appendix Section G that this symmetry characterizes the terms in real output or marginal costs in the Taylor pricing framework. It looks like price rigidity alone is an insufficient deviation from market efficiency to support an upward sloping Phillips curve. This will surprise many but should become a central tenant of modern Keynesian economics. Finally, subject to the other optimality conditions, the ideal represented by (5) can be interpreted as enforcing output neutrality.
10.3.2 Other Coefficients and Trade-OffsThis final part discusses salient features contained in the remaining slope coefficients. It is supported by Appendix G.2 that reminds readers of the basic Taylor pricing format.
\
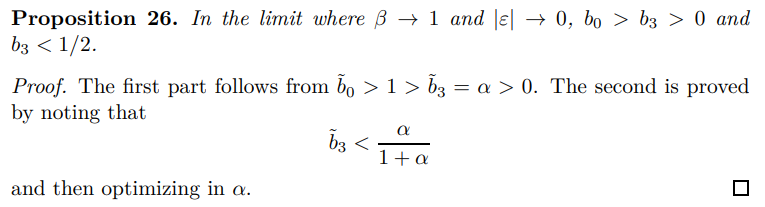
\ This is the idea that in the patient limit, inflation is equally sensitive to announced stimulus policies, no matter how far into the future they are realised.[98]
\ This is a figment of the lack of inter-temporal distortions on the singular surface of Calvo and the lack of staggered optimization under Rotemberg.
\ The over-weighting of past relative to future inflation contrasts with Taylor pricing, where they are always given equal weighting. In fact there is an interesting trade-off here. Calvo contains only one lag but gives it extra importance in the pricing decision, whereas Taylor contains the same or more lags but current inflation determination must be balanced between past lags and future expectations. This is an interesting point of empirical departure between the two prominent inflation frameworks.
\ The lagged inflation coefficient holds the key trade-off of monetary policy design. A more active effort to stabilize inflation, reflected in a higher aπ, leads to an inflation process that is more persistent and therefore more difficult to control. The Phillips curve is not policy invariant, as Lucas suspected. This has challenging econometric implications that I leave for future work.
\ Lastly, turning to the price dispersion effect, the first surprise is that its coefficient changes between the singular |ε| and correct approximations. Thus, this slow moving distortion term helps to reduce the positive persistence and surely makes the inflation process more forward-looking. Moreover, it is also governed by our neutrality result because in the limit α → 1 the |ε| approximation merges into the √ ε. With Taylor pricing again there is symmetry.
\ Finally, we arrive at the deepest generality of our results; there is Real Neutrality. Suppose that staggered nominal adjustment is added into an otherwise business cycle environment, such that there are no inter-temporal distortions. Current inflation is determined by a weighted average of past and future expected inflation, whilst the coefficients on real shocks net out. This is modern Keynesian economics’ answer to the Classical Dichotomy that inflation is determined by the money supply rather than real output. Verily this is a firm basis for a New Neo-Classical Synthesis.
\
:::info This paper is available on arxiv under CC 4.0 license.
:::
[95] Appendix I.2 contains more information on this argument.
\ [96] They typically put more emphasis on financial market factors that sound like modern behavioural economics with alternative policy prescriptions.
\
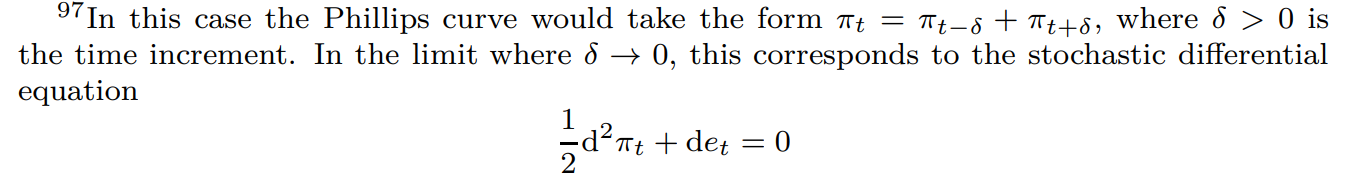
\ Nevertheless, there may be better limiting arguments down which to address the model in continuous time, which allow consideration of α bounded away from one.
\ [98] The idea was popularized by Del Negro et al. [2023]. It comes about from the alternative forward expansion
\
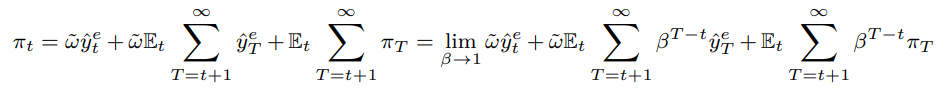
\ It is roundly rejected on the data for a variety of tests (see Coibion et al. [2023], Swanson [2021] and Bhattarai and Neely [2022]).
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright , Central Coast Communications, Inc.