Mathematical Proofs for SPD Inner Products and Pseudo-Gyrodistances in Manifold Layers

Table of Links

Abstract and 1. Introduction

2. Preliminaries

3. Proposed Approach

   3.1 Notation

   3.2 Nueral Networks on SPD Manifolds

   3.3 MLR in Structure Spaces

   3.4 Neural Networks on Grassmann Manifolds

4. Experiments

5. Conclusion and References

A. Notations

B. MLR in Structure Spaces

C. Formulation of MLR from the Perspective of Distances to Hyperplanes

D. Human Action Recognition

E. Node Classification

F. Limitations of our work

G. Some Related Definitions

H. Computation of Canonical Representation

I. Proof of Proposition 3.2

J. Proof of Proposition 3.4

K. Proof of Proposition 3.5

L. Proof of Proposition 3.6

M. Proof of Proposition 3.11

N. Proof of Proposition 3.12

I PROOF OF PROPOSITION 3.2

Proof. We first recall the definition of the binary operation ⊕g in Nguyen (2022b).

\

\

\

J PROOF OF PROPOSITION 3.4

Proof. The first part of Proposition 3.4 can be easily verified using the definition of the SPD inner product (see Definition G.4) and that of Affine-Invariant metrics (Pennec et al., 2020) (see Chapter 3).

\ To prove the second part of Proposition 3.4, we will use the notion of SPD pseudogyrodistance (Nguyen & Yang, 2023) in our interpretation of FC layers on SPD manifolds, i.e., the signed distance is replaced with the signed SPD pseudo-gyrodistance in the interpretation given in Section 3.2.1. First, we need the following result from Nguyen & Yang (2023).

\ \

\ \ We consider two cases:

\ \

\ \ \

K PROOF OF PROPOSITION 3.5

Proof. This proposition is a direct consequence of Proposition 3.4 for β = 0.

\

L PROOF OF PROPOSITION 3.

Proof. The first part of Proposition 3.6 can be easily verified using the definition of the SPD inner product (see Definition G.4) and that of Log-Cholesky metrics (Lin, 2019).

\ To prove the second part of Proposition 3.6, we first recall the following result from Nguyen & Yang (2023

\ \

\ \ According to our interpretation of FC layers,

\ \

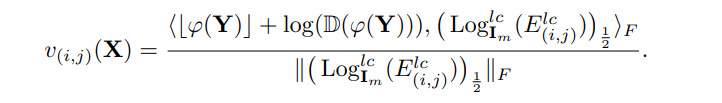
\ \ We consider two cases

\ \

\ \ \

M PROOF OF THEOREM 3.1

\

\ \ \

\ \ \

\ \ \

N PROOF OF PROPOSITION 3.12

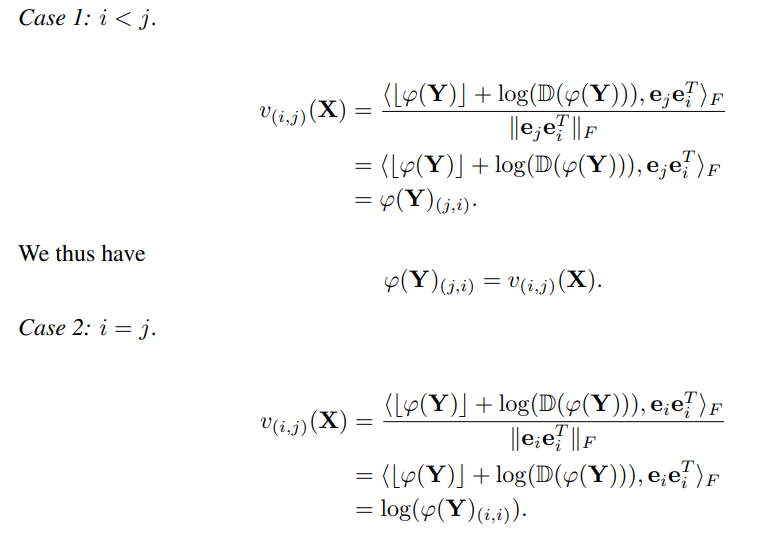
Proof. We need the following result from Nguyen & Yang (2023).

\ \

\ \ \

\ \ \

\ \ \

\ \ \

:::info Authors:

(1) Xuan Son Nguyen, ETIS, UMR 8051, CY Cergy Paris University, ENSEA, CNRS, France ([email protected]);

(2) Shuo Yang, ETIS, UMR 8051, CY Cergy Paris University, ENSEA, CNRS, France ([email protected]);

(3) Aymeric Histace, ETIS, UMR 8051, CY Cergy Paris University, ENSEA, CNRS, France ([email protected]).

:::

:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.

:::

\