and the distribution of digital products.
Keeping Time on the Moon: A Relativistic Approach to Lunar Clocks
Clocks at Earth-Moon Lagrance Points
4.1 Clock at Lagrange point L1
\ Appendix 1: Fermi Coordinates with Origin at the Center of the Moon
Appendix 2: Construction of Freely Falling Center of Mass Frame
Appendix 3: Equations of Motion of Earth and Moon
Appendix 4: Comparing Results in Rotating and Non-Rotating Coordinate Systems
Acknowledgments and References
\
APPENDIX 1: FERMI COORDINATES WITH ORIGIN AT THE CENTER OF THE MOON
\ We give the transformation equations between barycentric coordinates and Fermi normal coordinates with the center at the Moon as follows:[6]
\
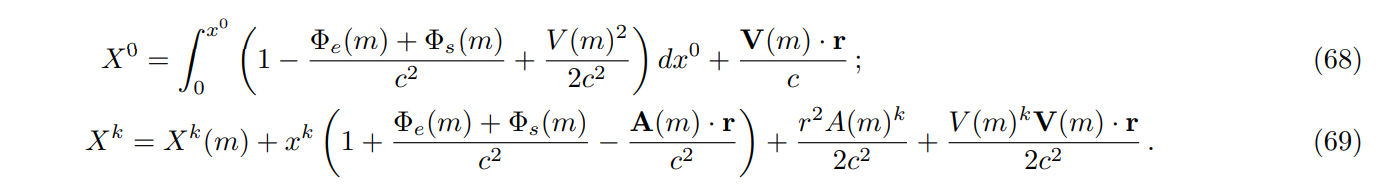
\ Here, the notation (m) as in V(m) represents quantities evaluated at the Moon’s center of mass. The quantity V (m) is the magnitude of the Moon’s velocity. Transformation coefficients can be derived and are:
\
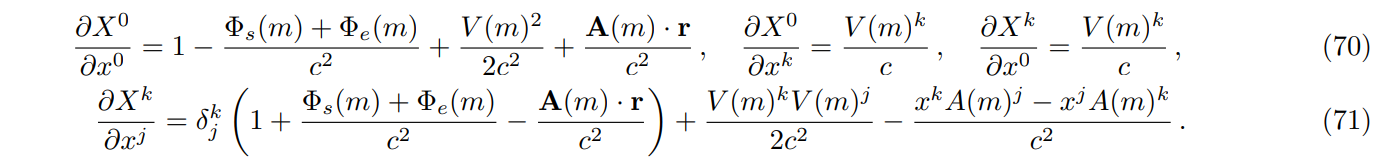
\ Transformation of the metric tensor is accomplished with the usual formula:
\
\ where the summation convention for repeated indices applies. Thus, for the time-time component of the metric tensor in the freely falling frame,
\
\
\
\
\
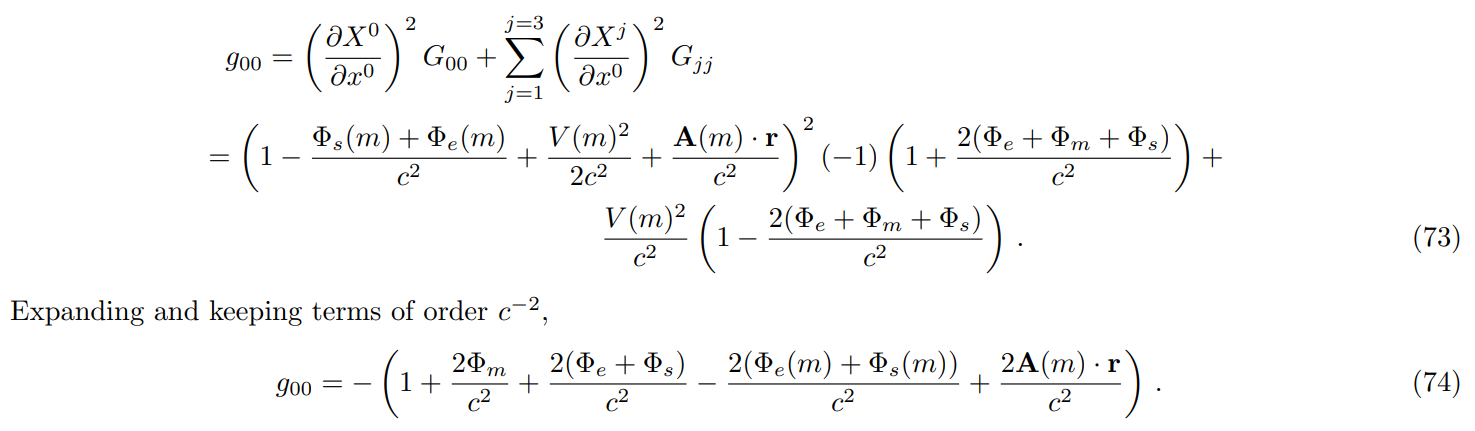
\ \ The transformation coefficients are easily obtained from the above coordinate transformations and are
\
\
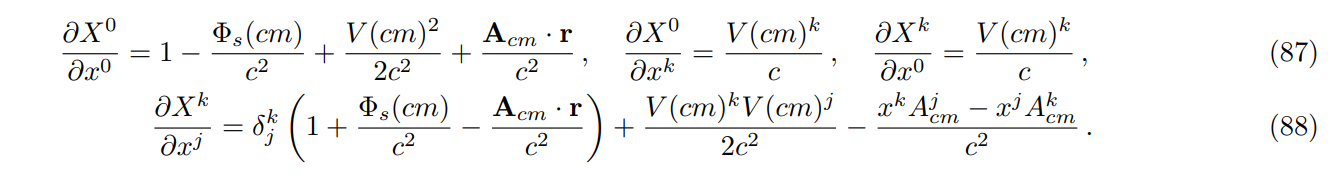
\ \ Transformation of the metric tensor using Eq. (72): the metric component g00 in the center of mass frame,
\
\
\
\
\
\
\
\
\
\
\
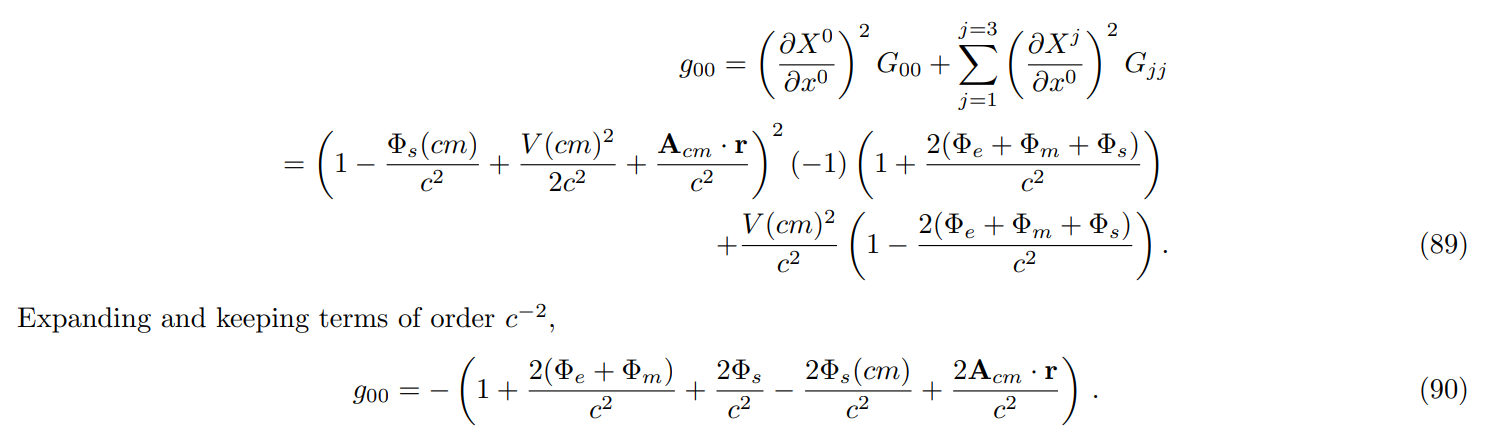
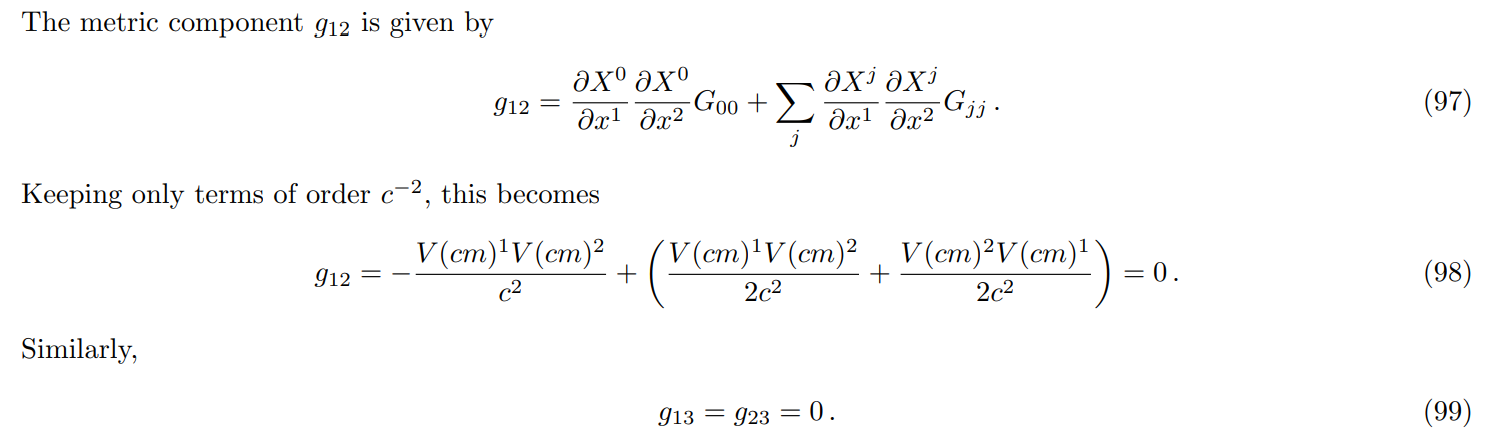
\ \ Summarizing, the scalar invariant in the center of mass system is
\
\
\ \
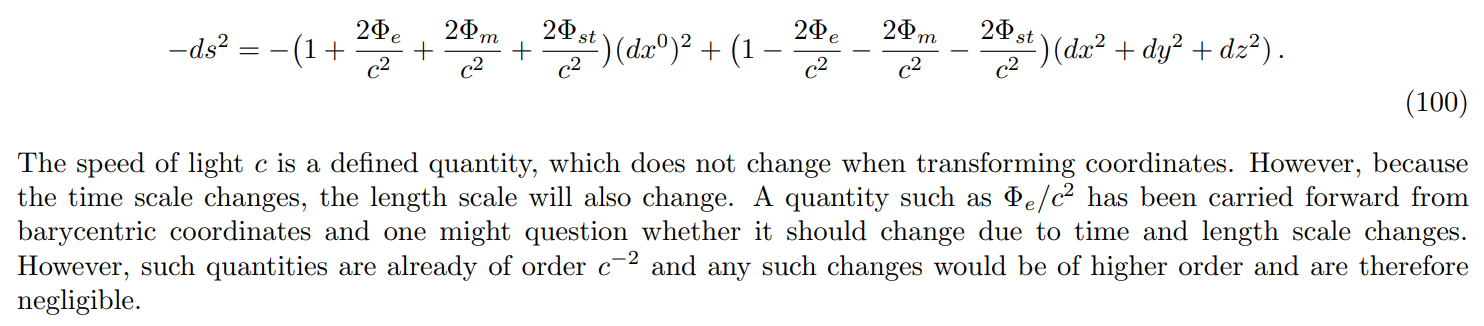
:::info Authors:
(1) Neil Ashby, National Institute of Standards and Technology, Boulder, CO 80305 ([email protected]);
(2) Bijunath R. Patla, National Institute of Standards and Technology, Boulder, CO 80305 ([email protected]).
:::
:::info This paper is available on arxiv under CC0 1.0 license.
:::
\