Improved BGPLVM for scRNA-seq: Pre-Processing and Likelihood

Abstract and 1. Introduction

2. Background

2.1 Amortized Stochastic Variational Bayesian GPLVM

2.2 Encoding Domain Knowledge through Kernels

3. Our Model and Pre-Processing and Likelihood

3.2 Encoder

4. Results and Discussion and 4.1 Each Component is Crucial to Modifies Model Performance

4.2 Modified Model achieves Significant Improvements over Standard Bayesian GPLVM and is Comparable to SCVI

4.3 Consistency of Latent Space with Biological Factors

4. Conclusion, Acknowledgement, and References

A. Baseline Models

B. Experiment Details

C. Latent Space Metrics

D. Detailed Metrics

In the sections below, we discuss a set of modifications to the baseline model presented above, which form the main contributions of this work. In particular, we show that row (library) normalizing the data, using an appropriate likelihood, incorporating batch and cell-cycle information via SE-ARD+Linear and PerSE-ARD+Linear (Section 2.2) and implementing a modified encoder significantly improves the BGPLVM’s performance. We present the schematic of the modified BGPLVM in Figure 1.

Raw scRNA-seq data are discrete and must be pre-processed to better align with the Gaussian likelihood in the probabilistic model of the baseline discussed above, which we call OBGPLVM (short for Original Bayesian GPLVM). However, the assumption that this pre-processed data are normally distributed is not necessarily justified. Instead of adjusting the data to fit our model, we aim to better adapt our likelihood to the data. In particular, we only normalize the total counts per cell (i.e. library size) to account for technical factors (Lun et al., 2016) and adopt a negative binomial likelihood like that in scVI (detailed in Appendix A.1).

\

\ In our initial experiments, we found that the more complex the likelihood function was (in terms of parameters to be learned), the worse the resulting BGPLVM-learned latent space was. While one may expect the more complex and expressive likelihoods to perform better, this opposite trend may be because the model is non-identifiable. That is, especially since the loss function does not explicitly optimize for latent space representations, the extra parameters may overfit and cause the model to fail to learn important biological signals. One such ablation study is presented in Appendix B.3.2. Due to this observation, we focus on the simplest (and best performing) negative binomial based likelihood, ApproxPoisson.

\

:::info This paper is available on arxiv under CC BY-SA 4.0 DEED license.

:::

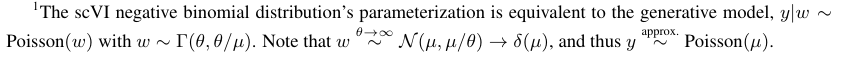
:::info Authors:

(1) Sarah Zhao, Department of Statistics, Stanford University, ([email protected]);

(2) Aditya Ravuri, Department of Computer Science, University of Cambridge ([email protected]);

(3) Vidhi Lalchand, Eric and Wendy Schmidt Center, Broad Institute of MIT and Harvard ([email protected]);

(4) Neil D. Lawrence, Department of Computer Science, University of Cambridge ([email protected]).

:::

\