and the distribution of digital products.
How Other Planets and Their Moons Sabotage Our Search for Earth Twins
- Diffraction Limit Comparisons for Future Telescopes
- Photobombing in our Solar System
- Consequences for Obtained Spectra
- Mitigation Strategies and Discussion, and References
The theoretical minimum diffraction-limited angular resolution a telescope can resolve is related to the wavelength of observation and the diameter of the entrance aperture of the primary objective, typically the telescope mirror. For space telescopes that aim to observe potentially rocky planets in a system’s habitable zone in visible or near-infrared light, this contributes to/helps set limits on both the minimum Inner Working Angle (IWA) (the λ/d distance at which off-axis throughput of a coronagraphic system > 50%, where λ is the wavelength of interest and d is the diameter of the entrance aperture of the primary objective - note that this is mask dependent) and angular size of the point spread function of an object of interest that exceeds the contrast floor for the telescope (Traub & Oppenheimer 2010). This heavily influences yields for a given telescope that is attempting to observe specific classes of planets (Stark et al. 2019).
\ The diffraction limit of a telescope also influences characterization of a target because minimum PSF size corresponds to a physical distance below which additional sources (such as additional planets/a moon) cannot be resolved. Previous studies have demonstrated an unresolved moon may contribute to an obtained spectra for a planet in ways that complicate interpretation and produce false positive molecular detections (Robinson 2011; Rein et al. 2014). We examine how the diffraction limit for a hypothetical Decadal-like 6m space telescope may influence PSF size for targets of interest for a range of potential planetary systems with different host stars at different distances. In figure 1, we compare diffraction limits to two distances for which we are concerned with ’photobombing’ - the Hill radius of an Earth-twin planet relevant to moons, and the HZ width for the system, relevant to other potentially unresolvable planets within the PSF. Note that this theoretical diffraction limited PSF size is optimistic since coronagraph masks can broaden PSF size by, for example, effectively decreasing the pupil diameter.(private communication, Neil Zimmerman)
\ We calculated the diffraction limits (blue/red horizontal lines in figure 1) using the formula for the first zero-intensity angle for a clear circular aperture (≈ 1.22λ/d), which gives an estimate of the distance over which an additional object may not be distinguishable within a PSF. However, intensity drops off from PSF’s central peak with a full-width at half-maximum at ≈ 80% of that value. This may have implications on extricating potential photobombing signals (see section 5). For reference wavelengths, we use minimum/maximum wavelengths from two direct imaging mission studies commissioned for the Decadal: HabEx (Gaudi et al. 2020) and LUVOIR (The LUVOIR Team 2019), which corresponds to 200 nm and 2.5 µm for the Extreme Coronagraph for Living Planetary Systems instrument on LUVOIR. We modeled the diffraction limit and other distance calculations for systems out to 50 parsecs, based on the cutoff used to maximize Exo-Earth yield in a previous study (Stark et al. 2014).
\
\
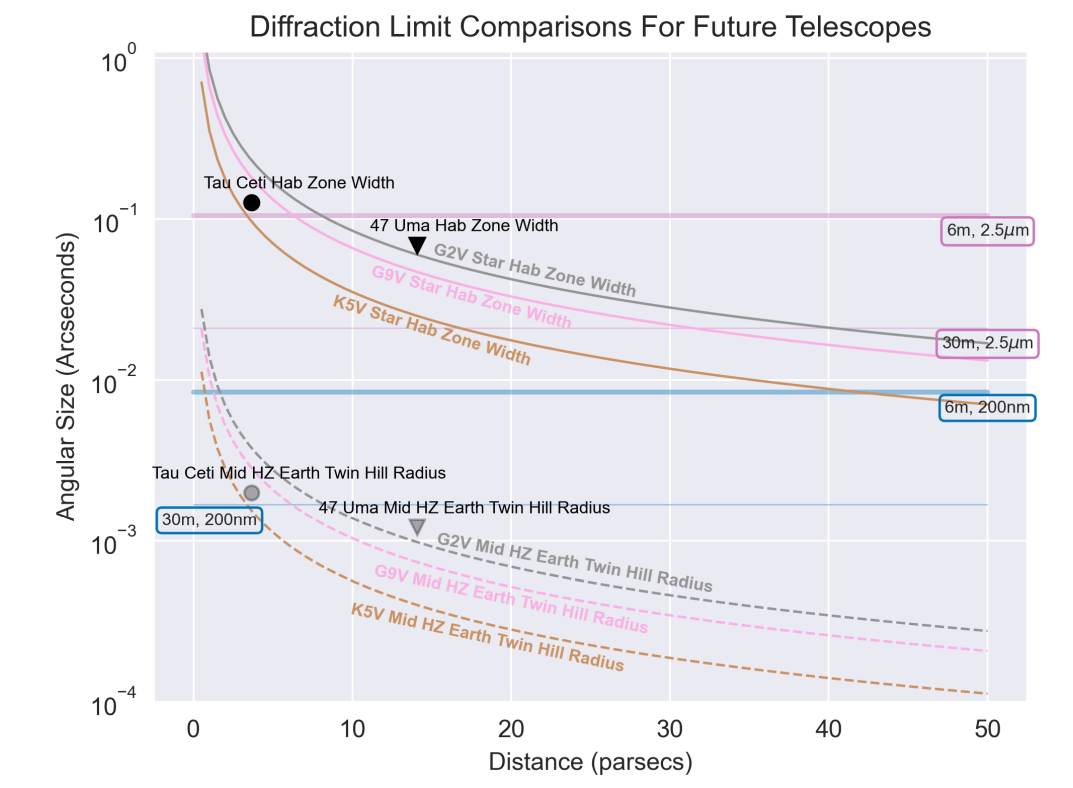
\ There are several implications of the comparisons in figure 1:
\
The diffraction limit for a 6m class telescope is larger than HZ width for Sun-like and smaller stars in the infrared for many of the distances examined. While the diffraction limit for 2.5 µm is clearly larger than the HZ for all three stars at distances ≈> 10pc, the diffraction limit for 1.0 µm is ≈ equal to HZ width for the G9V and G2V system at ≈ 25 and 35 pc, respectively. Note the diffraction limit is the one-sided distance from central peak to first minima in the Airy disk, so the more appropriate comparison for PSF width versus HZ width may be 2*diffraction limit, which suggests even closer distances would have commensurate sizes for these two values. For a 30m telescope, the diffraction limit does not equal HZ width until about 50 pc away for 2.5 µm, thus next generation large ground telescopes with adaptive optics may potentially aid in constraining planet position.
\
For a mid-HZ target in a case where the diffraction limit size ≈ HZ width, the PSF would contain additional habitable zone objects that fall within the PSF in the direction of orbital motion as well. For cases where the diffraction limit is larger than HZ width or the target is closer to a HZ edge with a significant PSF size, potential photobombing planets may include those outside the HZ and unless there are ideal observational conditions, there may be significant uncertainty in the targets’ estimated orbital separation. The climate of planets is sensitive to orbital separation as it determines incoming stellar flux received - supplementary orbit constraining measurements using radial velocity and astrometry may be critical.
\
- For a decadal-like telescope, at basically all wavelengths at relevant distances examined, the Hill sphere for a mid-HZ Earth-twin is significantly smaller than the diffraction limit. This reinforces previous studies’ findings that a bound moon would be difficult to image from a planet, particularly since bound moons are likely to exist at a fraction of the hill radius distance. Only for the closest distances at the bluest wavelengths does the 30m telescope come close to being able to probe the hill sphere.
\
:::info Author:
(1) Prabal Saxena, CRESST II/University of Maryland, College Park, Maryland 20742, USA and NASA Goddard Space Flight Center, Greenbelt, Maryland 20771, USA ([email protected]).
:::
:::info This paper is available on arxiv under ATTRIBUTION-SHAREALIKE 4.0 INTERNATIONAL license.
:::
\