How (K-)SIF Outperforms FIF in Real-Data Anomaly Detection

:::info Authors:

(1) Guillaume Staerman, INRIA, CEA, Univ. Paris-Saclay, France;

(2) Marta Campi, CERIAH, Institut de l’Audition, Institut Pasteur, France;

(3) Gareth W. Peters, Department of Statistics & Applied Probability, University of California Santa Barbara, USA.

:::

Abstract and 1. Introduction

2. Background & Preliminaries

2.1. Functional Isolation Forest

2.2. The Signature Method

3. Signature Isolation Forest Method

4. Numerical Experiments

4.1. Parameters Sensitivity Analysis

4.2. Advantages of (K-)SIF over FIF

4.3. Real-data Anomaly Detection Benchmark

5. Discussion & Conclusion, Impact Statements, and References

\ Appendix

A. Additional Information About the Signature

B. K-SIF and SIF Algorithms

C. Additional Numerical Experiments

To evaluate the effectiveness of the proposed (K-)SIF algorithms and provide a comparison with FIF, we perform a comparative analysis using ten anomaly detection datasets constructed in Staerman et al. (2019) and sourced from the UCR repository (Chen et al., 2015). In contrast to Staerman et al. (2019), we do not use a training/test part since the labels are not used for the training and train and evaluate models on the training data only. We evaluate the algorithms’ performance by quantifying the AUC under the ROC curves.

\

\

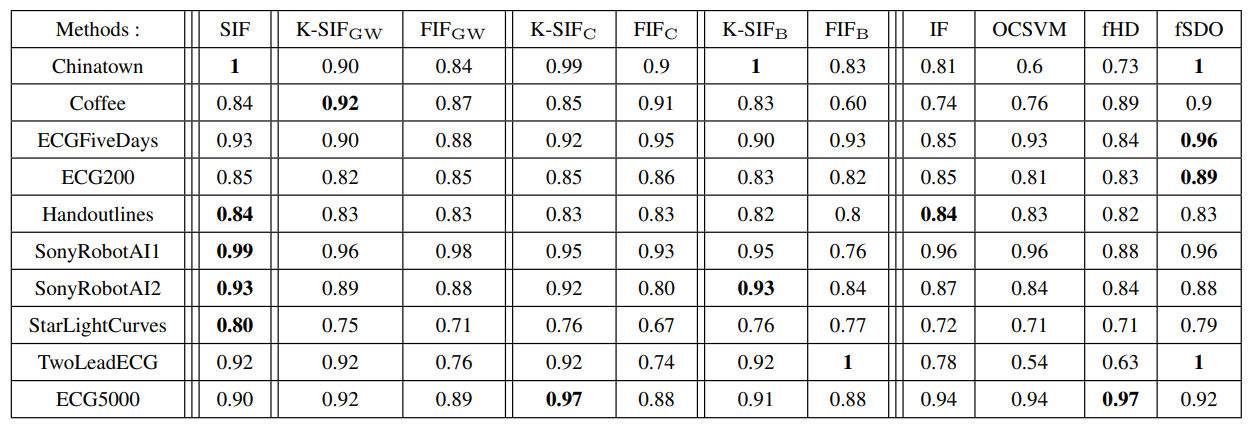
\ On one hand, Figure 4 illustrates the performance disparity between FIF and K-SIF using the Brownian dictionary. Notably, K-SIF exhibits a significant performance advantage over FIF. This observation underscores the effectiveness of the signature kernel in improving FIF’s performance across most datasets, emphasizing the advantages of utilizing it over a simple inner product. On the other hand, considering the intricacy of functional data, no unique method is expected to outperform others universally.

\ However, SIF demonstrates strong performance in most cases, achieving the best results for five datasets. In contrast to FIF and K-SIF, it shows robustness to the variety of datasets while not being drastically affected by the choice of the parameters involved in FIF (dictionary and inner product) and K-SIF (dictionary).

\

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\