and the distribution of digital products.
DM Television
How Do Household Preferences Shape Economic Models?
:::info Author:
(1) David Staines.
:::
Table of Links4 Calvo Framework and 4.1 Household’s Problem
4.3 Household Equilibrium Conditions
4.5 Nominal Equilibrium Conditions
4.6 Real Equilibrium Conditions and 4.7 Shocks
5.2 Persistence and Policy Puzzles
6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems
7 General Linearized Phillips Curve
8 Existence Results and 8.1 Main Results
9.2 Algebraic Aspects (I) Singularities and Covers
9.3 Algebraic Aspects (II) Homology
9.4 Algebraic Aspects (III) Schemes
9.5 Wider Economic Interpretations
10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs
10.4 Microeconomic Interpretation
\ Appendices
A Proof of Theorem 2 and A.1 Proof of Part (i)
B Proofs from Section 4 and B.1 Individual Product Demand (4.2)
B.2 Flexible Price Equilibrium and ZINSS (4.4)
B.4 Cost Minimization (4.6) and (10.4)
C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence
D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium
D.2 Profits and Long-Run Growth
E Slopes and Eigenvalues and E.1 Slope Coefficients
E.4 Rouche’s Theorem Conditions
F Abstract Algebra and F.1 Homology Groups
F.4 Marginal Costs and Inflation
G Further Keynesian Models and G.1 Taylor Pricing
G.3 Unconventional Policy Settings
H Empirical Robustness and H.1 Parameter Selection
I Additional Evidence and I.1 Other Structural Parameters
I.3 Trend Inflation Volatility
4.2 PreferencesThe focus is on well-behaved models that readily generate unique interior solutions, to this end, I make several intuitive restrictions on preferences. To do so, I make several intuitive restrictions. To this end, u ′ > 0 so agents always wish to consume more and the transversality condition will bind with equality. u ′′ < 0 to incentivize consumption smoothing. It is costly for agents to work ν ′ > 0, ν ′′ > 0 encourages the agent to balance work and leisure.[22] Together these conditions ensure uniqueness of interior solutions to the agent’s optimization at any point in time with a non-stochastic background.
\ Additional conditions are required to rule out boundary solutions. The standard Inada condition for consumption is
\

\ along with zero net wealth. This ensures the representative household will always work. To force them to take leisure
\
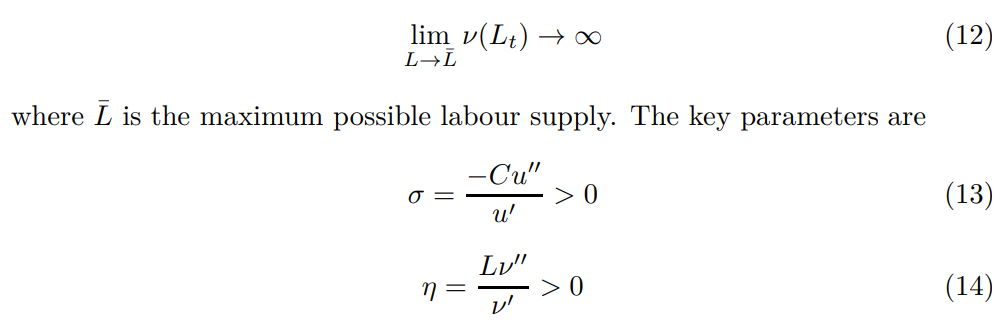
\ σ represents the coefficient of relative risk aversion. It is also the inverse of the elasticity of inter-temporal substitution. η is the inverse Frisch elasticity of labor supply. For the empirical part I will work with the popular functional forms. This ensures these parameters are structural and do not vary with income allowing comparison with standard econometric estimates.[23]
\

\ Each firm produces an individual variety for which demand is given by
\
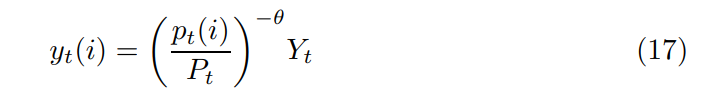
\ θ is the elasticity of demand. Appendix B.1.1 details the underlying optimization problem.
\
:::info Author:
(1) David Staines.
:::
:::info This paper is available on arxiv under CC 4.0 license.
:::
[22] Alternatively, we could imagine leisure is a good in demand that represents an opportunity cost of working. It will be convenient to do so in one proof discussed in the Appendix (C.1.2)
\

- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright , Central Coast Communications, Inc.