and the distribution of digital products.
DM Television
Game Theory and Blockchain: Why DAG-Protocol Fails Against Greedy Behavior
IX. Discussion and Future Work
V. GAME THEORETICAL ANALYSIS
\ We examine the following hypothesis:
\ Hypothesis 2. So-called (honest) H-behavior with RTS is a Subgame Perfect Nash Equilibrium (SPNE) in an infinitely
\
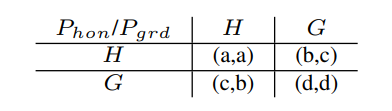
\ repeated DAG-PROTOCOL game. This was presented in Inclusive [26] and we will contradict it.
\ Generally speaking, any strategic profile s∗ becomes an equilibrium (SPNE) in an infinitely repeated game Γ if one of the following holds:
\ • s∗ is a Pure Nash Equilibrium (PNE) in the base (stage) Γ game. Then, s∗ is trivially a SPNE too.
\ • There exists an incentive making the rational players to agree on s∗. We recall so-called Folk theorem [16], [34] stating that any (individually) efficient profile may become a mutual agreement (a stable profile) if the players are willing to punish a player deviating from the agreement. Punishing is relevant only if the targeted player is farsighted enough. Let δ ∈ ⟨0, 1⟩ denote the discount factor [34] put by the player to her future profits.
\ We study the trustworthiness of Hypothesis 2 in the following analysis. Our goal is to find a principle that would ensure the H-behavior in some natural way (self-enforcing principle).
\ A. Model of the DAG-PROTOCOL
\ Let us assume a finite non-empty population of miners. We want to distinguish between honest (H) and greedy (G) behavior (i.e., behavioral phenotypes).
\ he nature of DAG-PROTOCOL imposes that players receive transaction fees after a certain delay (necessary to achieve consensus on the order of blocks). However, we can discretize the flow of transactions into atomic rounds of the game in order to simplify our analysis. This allows us to study the behavior of players within a well-defined time frames. In every round, players decide on their actions and receive payoffs consequently. Overall, we can model the situation as a repeated game with separate discrete rounds. Since no round is explicitly marked as the last one, this game is repeated infinitely. This allows us to analyze players’ behavior over an extended period of time, which is essential for understanding the long-term effects of different strategies.
\ We model DAG-PROTOCOL in the form of an infinitely repeated two players game with a base game
\

\ B. Analysis of the Model
\ For purposes of our analysis, lets start with the assumption that G-behavior is more attractive and profitable than H-behavior. Otherwise, there would be no reason to investigate
\

\ Hypothesis 2. Thus, let us consider c > a as the basic constraint. We also assume c > b, meaning that H-behavior loses against G-behavior in the cases of (H, G) and (G, H) profiles. These basic constraints yield the following scenarios:
\ • Scenario 1 (Tab. IIa): d > c > a > b,
\ • Scenario 2 (Tab. IIb): c > d > a > b,
\ • Scenario 3 (Tab. IIc): c > a > d > b,
\ • Scenario 4 (Tab. IId): c > a > b > d,
\ • Scenario 5 (Tab. IIe): where a = d and c > a, c > b.
\

\ Scenarios 1 and 2 are covered just for a sake of completeness. If the transaction fees were to cause such game outcomes, there would be no need to trust in H-behavior, and the system would settle in the unique (G, G) PNE. The behavior of players within Scenarios 3 and 4 is more complex. We analyze these scenarios in the following, while we present the circumstances needed for the profile (H, H) to become a stable outcome of the system. Scenario 5 is based on the constraint saying that the sum of all incoming transaction fees is constant in any set of rounds, therefore playing either (G, G) or (H, H) should generate the same profits.
\ 1) Scenario 3 (A) Purely Non-Cooperative Interpretation. Scenario 3 (Tab. IIc) represents a typical instance of so-called Prisoner’s dilemma [34], where cooperative profile (H, H) brings the highest social outcome; however, such a profile is unstable because each player does better if she deviates by playing G.
\ Claim 1. Players choose (G, G) in Scenario 3.
\ Proof: (Informal) Strategy G strictly dominates H and thus (G, G) is the unique PNE.
\ Corollary 1. If Phon wants to follow the social norm of DAGProtocol (which is irrational though) then Pgrd’s best response is pure G. If Phon is uncertain about her determination and plays randomly in mixed behavior (p, 1 − p), then Pgrd’s best response is pure G for any p ∈ ⟨0, 1⟩, where expected payoff from pure G is superior:
\
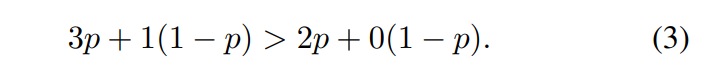
\ (B) When Some Coordination is Allowed. Let us introduce coordinated behavior into the game. Stability of (G, G) profile might now become possible in the context of Folk theorem if the following two conditions are fulfilled. (1) It must be common knowledge [5] that Phon adopts so called grim trigger strategy [34], [30], i.e., she plays H as long as Pgrd plays H, and once Pgrd deviates, then Phon turns into G-behavior forever, bringing the game into (G, G) profile. Player Pgrd is punished in this way. The first condition establishes a kind of agreement (a social norm) between players in this scenario. (2) Pgrd’s discount factor is higher than the minimal value δ:
\

\ E.g., a player i with δi = 0.5 is indifferent between receiving 100 in payoff now or 200 in the future. A player with δi → 0 does not bother about the future, i.e., setting agreements with such a player makes no sense.
\ The Folk theorem states that a player i with her δi > δ in the current round (e.g., the 1st round) prefers to play the agreed H because her expectation π((H, H), …) is higher than the profit from deviating the agreement and consequent punishments. This assumption is highly theoretical in our case, and we discuss it later in more detail (see Sec. V-C). Also, let us note that with increasing variance in transaction fees, the G behavior becomes more tempting, and thus it is difficult to believe that Pgrd’s discount factor exceeds the gap in Eq. 4.
\

\ Proof: (Informal) This situation might contain dynamic properties and vague interpretation
\

\

\ (B) When Some Coordination is Allowed. Similarly to Scenario 3 (see Sec. V-B1), let us assume (H, H) agreement to be a common knowledge to both players. Then, a punishment of the strategy G played by Phon should bring the game into (G, H) profile since H is Pgrd’s best response to G. The honest player factually improves her payoff by punishing her greedy opponent. Therefore, conclusion from Scenario 3 applies here in the same manner
\ 3) Scenario 5 (A) Purely Non-Cooperative Interpretation. Payoff functions in Scenario 5 come from our assumptions where players should obtain equal outcomes in profiles (H, H) and (G, G). The game is a Zero-sum game, meaning that no player can gain more than 100% profit, regardless of their chosen strategy since the sum of all incoming transaction fees is fixed in any set of rounds. As a result, the total profit for all players is always ”zero” (constant) if they all play H or G strategy. This scenario is similar to Scenario 3 (see Sec. V-B1). However, the concept of agreements and punishments loses any sense since (H, H) profile is not more socially efficient than (G, G)
\ Claim 3. (G, G) is the sole rational outcome of Scenario 5.
\ Proof: (G, G) is the unique PNE in Scenario 5
\ We might appeal for the responsibility of players who should refrain from playing G just because such a behavior negatively influences the reputation/popularity of DAG-Protocol in the long term. A dilemma of whether to utilize the shared resource in a reasonable or extensive way resembles the classical game-theoretical model called The Tragedy of Commons [31]. The honest player might insist on H, but it will only improve Pgrd’s payoff and damage Phon. That is why the game reaches stability only at (G, G)
\ In anonymous environments, individual interests are often prioritized over collective interests. This is because the lack of accountability makes it easier for individuals to act in their self-interest without any concerns about the welfare of the group. Therefore, collective action and cooperation might be very difficult to achieve in anonymous settings
\ C. Summary of Scenarios 1-5
\ Let us view DAG-PROTOCOL as a shared resource between miners, which enables them to earn some money. Any kind of player may utilize this resource anonymously (by PoW mining). The idea behind DAG-PROTOCOL claims that rational miners will not deplete this shared resource by extensive greedy play. If they deplete it, the resource is gone forever since the reputation of DAG-PROTOCOL is destroyed. Since players are rational, they are not supposed to let this happen. However, this theory stands on the assumption that this resource is the only job opportunity the miners have
\ The question we investigate is whether the DAGPROTOCOL is immune against greedy behavior. Intuitively, if it is not, then the resource might be fully depleted. Since in permissionless blockchains there is no technical way t stop the entrance of a greedy player, she might join DAGPROTOCOL. If the greedy behavior offers a better payoff (even temporary) then greedy miners might parasite on DAGPROTOCOL. Let us summarize our findings regarding the immunity of DAG-PROTOCOL against greedy behavior.
\ Claim 4. DAG-PROTOCOL is not a mechanism immune against greedy behavior.
\ We examined the DAG-PROTOCOL using five hypothetical scenarios and found out that:
\

\ 2) In Scenarios 3 and 4, stability in (H, H) profile can be achieved; however, it puts rather critical demands on the community of miners. They can theoretically enforce a greedy player to return into (H, H) by punishing her in (G, H) or (G, G) profiles. A rational player, who wants to stay or must stay in this repeated game forever, agrees upon (H, H) if (1) her discount factor is higher than a certain gap (see Eq. 4) and (2) punishing response from the community is guaranteed. The gap might also fluctuate depending on the current distribution of the transaction fees.[10] Nevertheless, the practical implementation of punishments has serious drawbacks:
\ a) Honest player can detect G-behavior only theoretically. In practical operation, the players can only guess from their previous payoffs that there is probably someone playing G in the system.
\ b) Greedy player can avoid punishment when she skips successive rounds and gains by doing something else (saving costs, mining on different blockchain, etc.). The Folk theorem applied here does not assume that the player can escape from the punishment.
\ c) Finally, the principle of punishment is to execute the G-behavior, which brings us to (G, G) at the end. There is no other more suitable tool for that. Basically, the honest player says ”do not play G, otherwise, I will play G as well”.
\ 3) Scenario 5 is based on the assumption that a Zero-sum game is the natural conclusion of PoW mining. Players gain equally in (H, H) and (G, G) profiles. The honest player risks a loss when playing H against the greedy player. This makes the (G, G) profile the only stable and rational outcome of this scenario. Scenario 5 has a strategic character of Tragedy of the Commons, where depletion of the shared resource is inevitable.
\ Corollary 2. We conclude that Hypothesis 2 is not valid. The (H, H) profile is not a PNE in any of our scenarios. Incentives enforcing H-behavior are hardly feasible in the anonymous (permissionless) environment of blockchains. A community of honest miners can follow the DAG-PROTOCOL until the attacker appears. The attacker playing the G strategy can parasite on the system and there is no defense against such a behavior (since greedy miners can leave the system anytime and mine elsewhere, which is not assumed in [26]). Therefore, H is not an evolutionary stable strategy [41], and thus H does not constitute a stable equilibrium.
\
:::info Authors:
(1) Martin Peresıni, Brno University of Technology, Faculty of Information Technology ([email protected]);
(2) Ivan Homoliak, Brno University of Technology, Faculty of Information Technology ([email protected]);
(3) Federico Matteo Bencic, University of Zagreb, Faculty of Electrical Engineering and Computing ([email protected]);
(4) Martin Hruby, Brno University of Technology, Faculty of Information Technology ([email protected]);
(5) Kamil Malinka, Brno University of Technology, Faculty of Information Technology ([email protected]).
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
Note that we consider DAG-based designs (described in Sec. IV) under this generic term of DAG-PROTOCOLS to simplify the description but not to claim that all DAG-PROTOCOLS (with RTS) can be modeled as we do.
\
Even though consensus protocols might contain multiple players, they might represent only one of two behavioral phenotypes, which is sufficient for us to prove the feasibility of our attack in our game theory model.
\
A distribution of the transaction fees is not the subject of a gametheoretical analysis but empirical evaluation presented later (see Sec. VII).
\
- Home
- About Us
- Write For Us / Submit Content
- Advertising And Affiliates
- Feeds And Syndication
- Contact Us
- Login
- Privacy
All Rights Reserved. Copyright , Central Coast Communications, Inc.