and the distribution of digital products.
The Case for Lagrange Points As Ideal Locations for Space Clocks
Clocks at Earth-Moon Lagrance Points
4.1 Clock at Lagrange point L1
\ Appendix 1: Fermi Coordinates with Origin at the Center of the Moon
Appendix 2: Construction of Freely Falling Center of Mass Frame
Appendix 3: Equations of Motion of Earth and Moon
Appendix 4: Comparing Results in Rotating and Non-Rotating Coordinate Systems
Acknowledgments and References
\
4. CLOCKS AT EARTH-MOON LAGRANGE POINTSThe Lagrange points offer a cost-effective and low-noise environment for stationing spacecraft with clocks because there is no net acceleration. As a result, the orbits of clocks at these points with respect to the Earth-Moon barycenter are well-determined and the corresponding frequency offsets are precisely determined. Therefore, the proper times of clocks at Lagrange points can be related to the proper times of clocks on the Earth and Moon with high precision. This information is crucial for synchronizing remote clocks in cislunar space. Both L4 and L5 are stable points, but L1 and L2 are only metastable locations.
4.1 Clock at Lagrange point L1In this section, we consider a clock at L1 and compare its rate to a clock on Earth’s surface. It is most convenient to use a freely falling inertial frame centered at the center of mass of the Earth-Moon system for this calculation. First, we need the precise position of L1; most treatments assume circular motion, but this is inadequate for our purposes. We assume Keplerian elliptical orbits for the Earth and Moon about the center of mass, for which the Earth-Moon distance is given by Eq. (19). The radial velocity is then
\
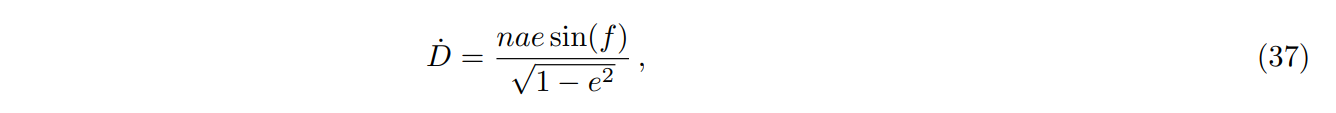
\ and the radial acceleration of the Moon relative to Earth is
\
\
\
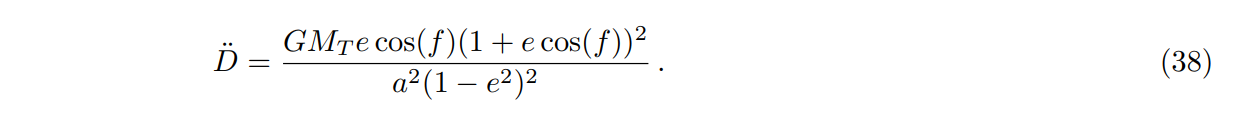
\ Assume that L1 is between the Earth and Moon and at a distance x1D from the Moon, the net gravitational force towards the Moon supplies the radial acceleration of L1, diminished by the centripetal acceleration due to rotation of the Earth-Moon line. This gives the condition
\
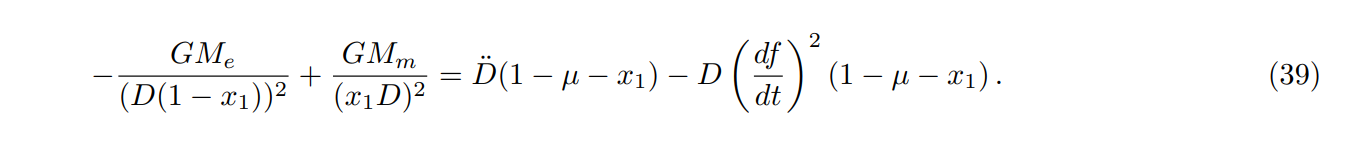
\ Solving Eq. (39) for x1 gives
\ x1 = 0.15093428(1).
\ The metric, neglecting solar tides, is
\
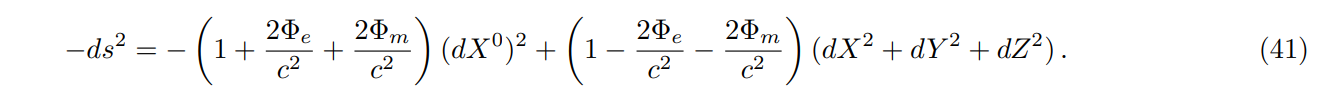
\ The motion is so slow that the potential terms in the last line can be neglected. The transverse and radial velocities of the clock due to the rotation of the Earth-Moon line are
\
\ So, the total velocity squared is
\
\
\
\
\
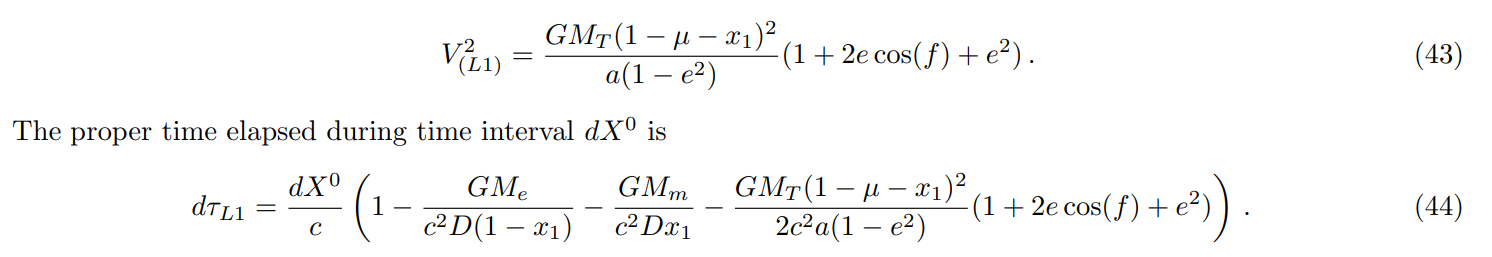
4.2. Clock at Lagrange point L2\
\
\
\
\
4.3. Clock at Lagrange point L4 or L5The clock is equidistant from Earth and the Moon. The total velocity squared is the sum of the radial velocity squared and the transverse velocity squared:
\
\
\
\
\
\
\
\
\ \
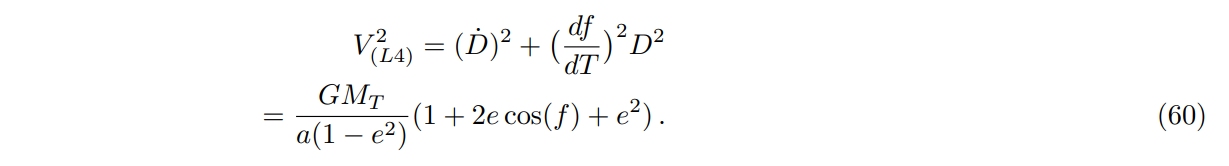
:::info Authors:
(1) Neil Ashby, National Institute of Standards and Technology, Boulder, CO 80305 ([email protected]);
(2) Bijunath R. Patla, National Institute of Standards and Technology, Boulder, CO 80305 ([email protected]).
:::
:::info This paper is available on arxiv under CC0 1.0 license.
:::
\