and the distribution of digital products.
Breaking the One-Size-Fits-All Model: Adaptive Merkle Trees for Blockchain Efficiency
:::info Authors:
(1) Oleksandr Kuznetsov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA and Department of Political Sciences, Communication and International Relations, University of Macerata, Via Crescimbeni, 30/32, 62100 Macerata, Italy ([email protected]);
(2) Dzianis Kanonik, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(3) Alex Rusnak, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA ([email protected]);
(4) Anton Yezhov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(5) Oleksandr Domin, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA.
:::
Table of Links1.1. The Blockchain Paradigm and the Challenge of Scalability
1.3. Our contribution and 1.4. Article structure
2. Conceptualizing the Problem
3. Our Idea for Optimizing Trees in Blockchain
4. Efficiency of adaptive Merkle trees
5. Algorithm for Merkle Tree Restructuring
6.2. Example 1.1: Binary Tree Restructuring Through Leaf Node Swapping
6.3. Example 2.1: Restructuring a Non-Binary Tree by Adding a Single Leaf
6.4. Example 2.2: Restructuring a Non-Binary Tree Through Leaf Pair Swapping
6.5. Example 2.3: Restructuring a Patricia-Merkle Tree Fragment Through Leaf Pair Swapping
7. Path Encoding in the Adaptive Merkle Tree
8.2. Technology and Advantages
9.2. Comparison with Existing Solutions
2. Conceptualizing the ProblemThe core issue addressed in this research is the optimization of tree structures in blockchain systems for efficient and cost-effective verification. Currently, blockchain data is stored in balanced trees, with Merkle paths for data verification being approximately equal in length and complexity across all data. This uniformity results in a consistent verification cost and complexity, regardless of the frequency of data use.
\ Figure 3 depicts a balanced Merkle Tree, a fundamental data structure used in blockchain for ensuring data integrity. Each leaf node (A-P) represents a block of data with a unique hash value, while the non-leaf nodes (AB, CD, etc.) are hashes of their respective child nodes. The root node (ABCDEFGHIJKLMNOP) encompasses the entire tree's hash, providing a single point of reference for the entire dataset's integrity.
\ The Merkle Tree's structure ensures that any alteration in a single data block can be quickly detected by recalculating the hashes up the tree to the root. However, this balanced structure, while efficient in evenly distributing the data, does not account for the frequency of data access or modification (frequency is indicated in brackets). As a result, frequently used data and rarely accessed data have the same level of complexity and cost in terms of verification, leading to inefficiencies in resource utilization.
\
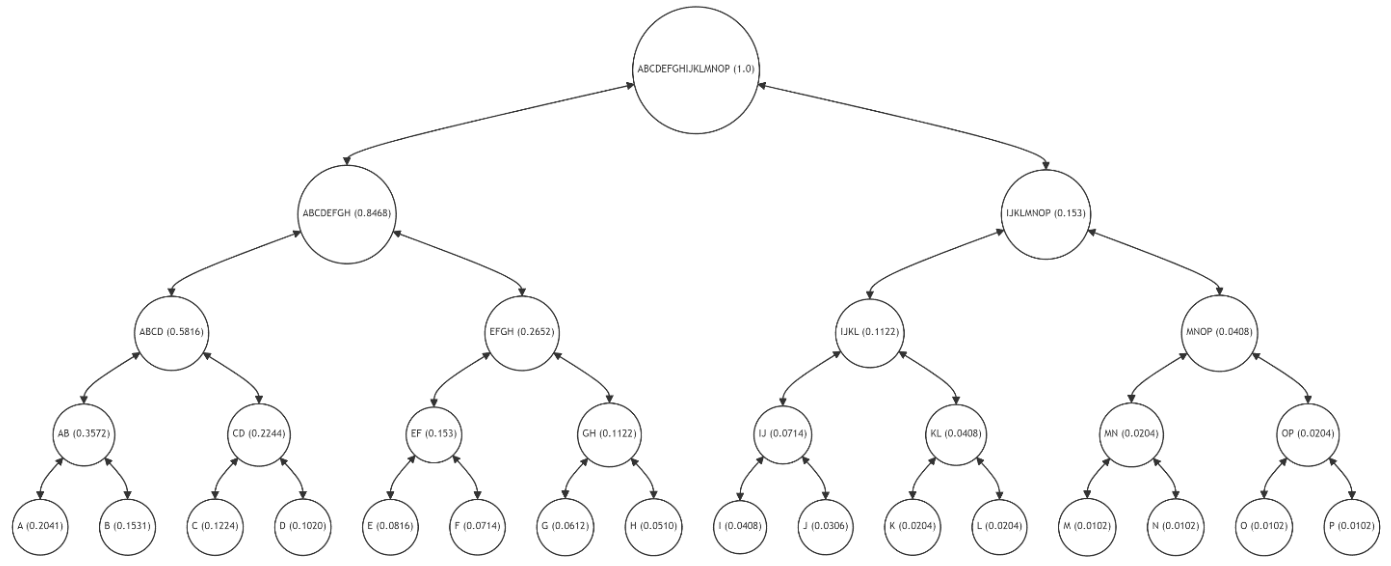
\ Figure 4 highlights the Merkle Path (nodes B, CD, EFGH, IJKLMNOP) for verifying the integrity of leaf node A (with a high frequency of 0.2041). The Merkle Path is marked in red, indicating the nodes whose hashes are required to verify A's integrity up to the root. The leaf node A and the root are highlighted in green, while the intermediate nodes (AB, ABCD, ABCDEFGH) involved in hash calculations are in yellow.
\ The verification process involves recalculating and comparing the hashes from node A up to the root, ensuring data integrity. However, this method, while straightforward, applies the same verification complexity to all data, regardless of usage frequency. This "one-size-fits-all" approach is suboptimal, especially for data that is accessed and modified frequently, as it incurs unnecessary computational overhead.
\
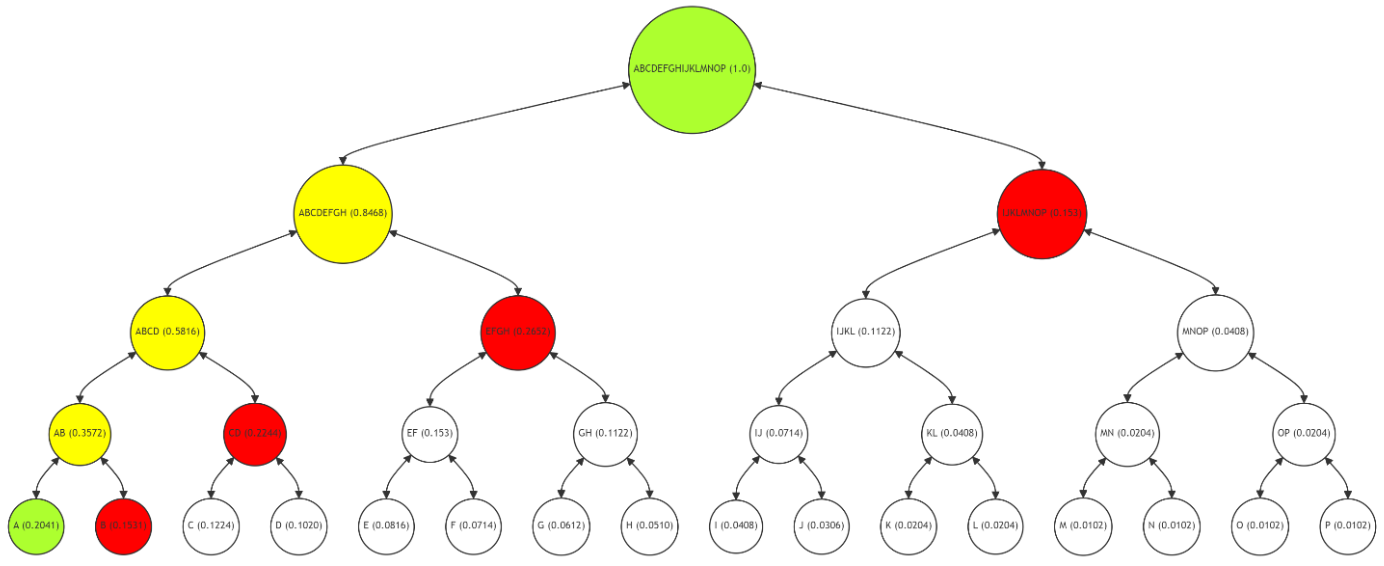
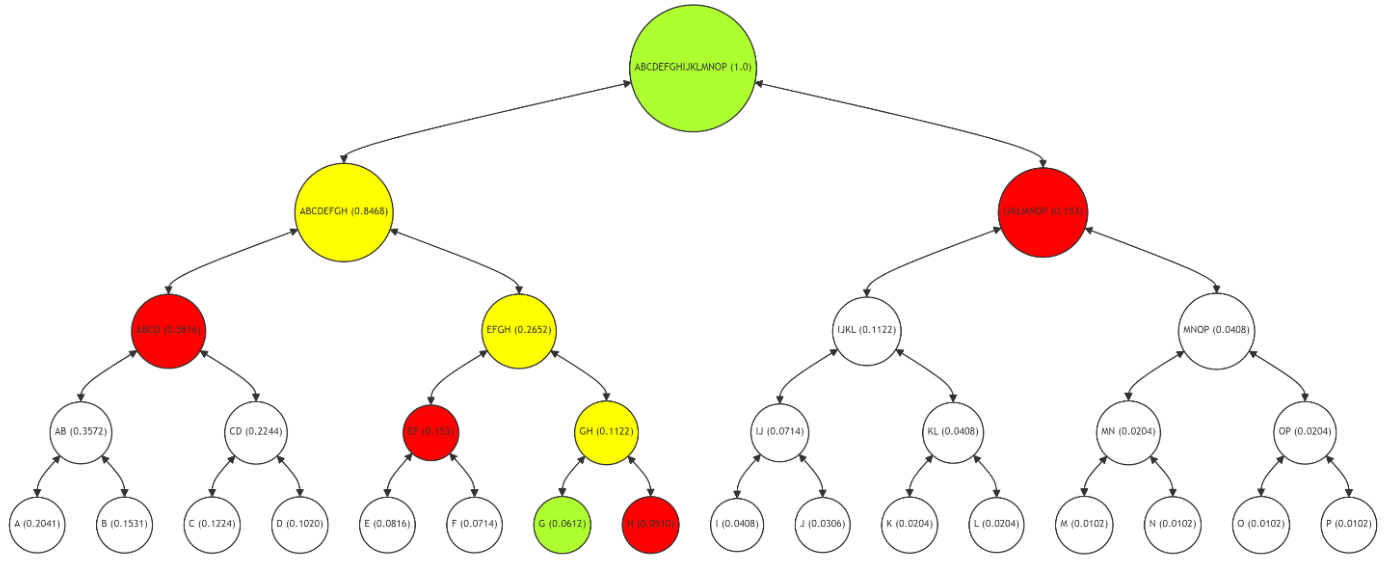
\ In Figure 5, the Merkle Path for verifying leaf node G (with a frequency of 0.0612) is shown. The path (nodes H, EF, ABCD, IJKLMNOP) is marked in red, with node G and the root in green, and the intermediate nodes (GH, EFGH, ABCDEFGH) in yellow. The verification process for G follows the same principle as for A, recalculating hashes along the red path to validate the data's integrity.
\
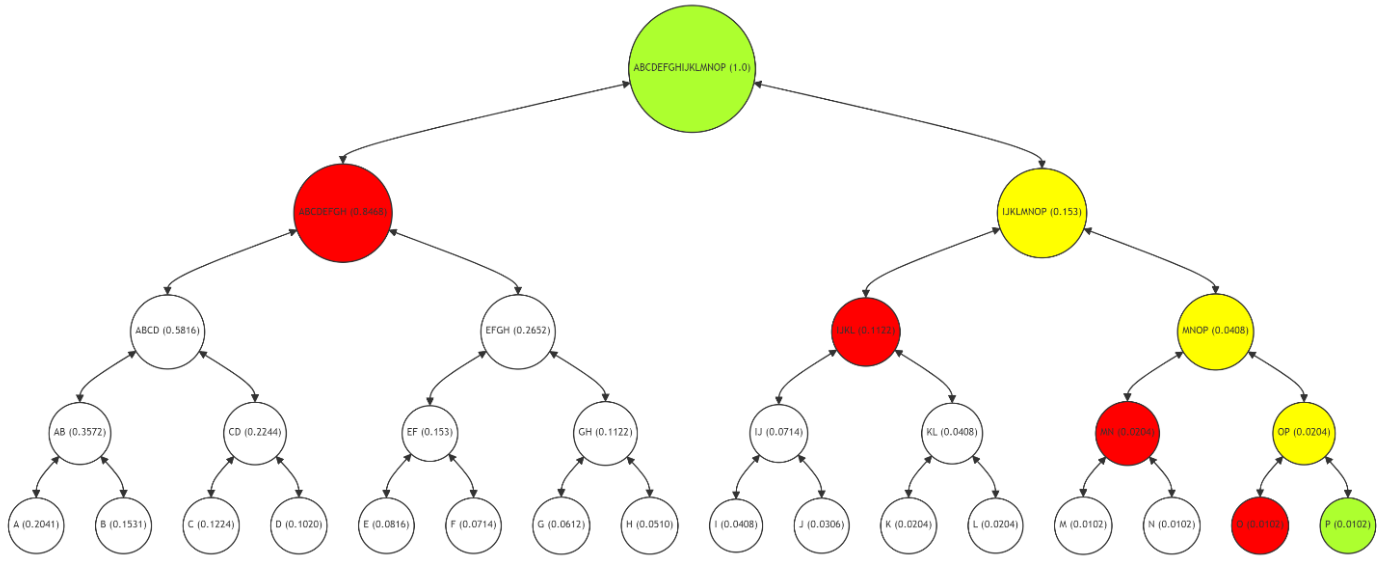
\ The Figure 6 demonstrates the Merkle Path for leaf node P (with a frequency of 0.0102), with the path (nodes O, MN, IJKL, ABCDEFGH) in red, P and the root in green, and intermediate nodes (OP, MNOP, IJKLMNOP) in yellow. The process for verifying P's integrity mirrors that of A and G, emphasizing the consistent approach across the tree.
\
\ This consistency in verification, while ensuring uniform security and integrity checks, does not account for the varying frequencies of data access and modification. It leads to a rigid and sometimes inefficient system, especially in a dynamic environment like blockchain, where data access patterns can vary significantly.
\ Thus, the current Merkle Tree verification process, as illustrated in these figures, is a rather primitive and blunt approach. It treats all data equally, irrespective of its usage frequency, leading to potential inefficiencies in computational resources. Our proposed solution aims to revolutionize this process by introducing adaptive Merkle Trees. These trees will optimize verification paths based on data usage frequency, significantly reducing the complexity and cost of verifying frequently accessed data. This innovative approach promises to enhance the efficiency and scalability of blockchain systems, tailoring the verification process to the dynamic needs of the network. By differentiating between frequently and infrequently accessed data, adaptive Merkle Trees can allocate computational resources more effectively, ensuring faster and more costefficient data verification. This method not only optimizes the blockchain's performance but also aligns with the evolving nature of blockchain usage, where certain data nodes may become hotspots of activity.
\
:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::
\