Breaking Down the Inductive Proofs Behind Faster Value Iteration in RL

:::info Authors:

(1) Jongmin Lee, Department of Mathematical Science, Seoul National University;

(2) Ernest K. Ryu, Department of Mathematical Science, Seoul National University and Interdisciplinary Program in Artificial Intelligence, Seoul National University.

:::

Abstract and 1 Introduction

1.1 Notations and preliminaries

1.2 Prior works

2 Anchored Value Iteration

2.1 Accelerated rate for Bellman consistency operator

2.2 Accelerated rate for Bellman optimality opera

3 Convergence when y=1

4 Complexity lower bound

5 Approximate Anchored Value Iteration

6 Gauss–Seidel Anchored Value Iteration

7 Conclusion, Acknowledgments and Disclosure of Funding and References

A Preliminaries

B Omitted proofs in Section 2

C Omitted proofs in Section 3

D Omitted proofs in Section 4

E Omitted proofs in Section 5

F Omitted proofs in Section 6

G Broader Impacts

H Limitations

First, we prove the following lemma by induction.

\

\

\

\

\

\

\

\

\ Now, we present our key lemmas for the first rate of Theorem 2.

\

\

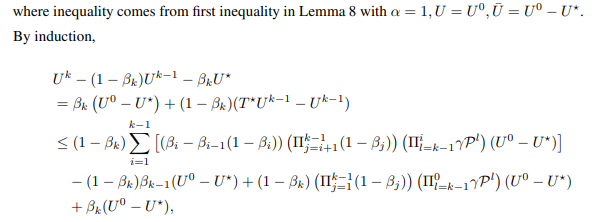
\ and let U¯ be the entire right hand side of inequality. Then, we have

\

\ By induction,

\

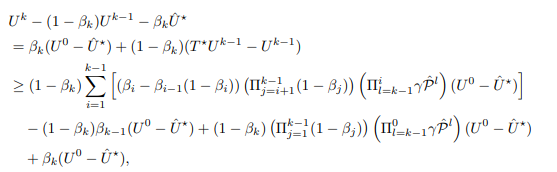
\ and let U¯ be the entire right hand side of inequality. Then, we have

\

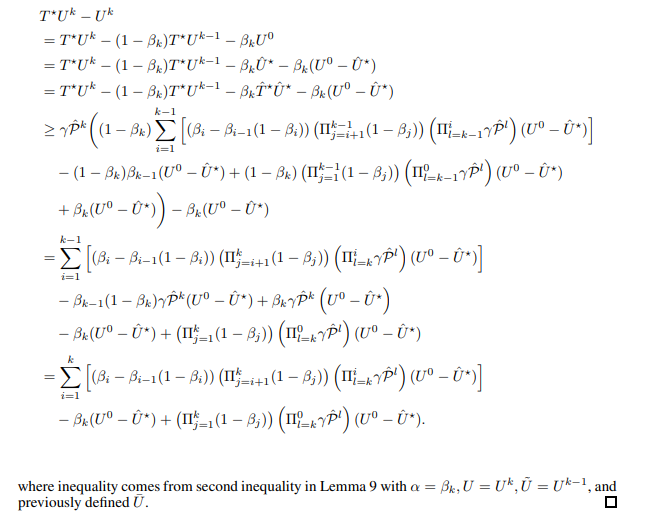
\ Now, we prove the first rate of Theorem 2.

\

\

\ where the second inequality is from the condition.

\ By induction,

\

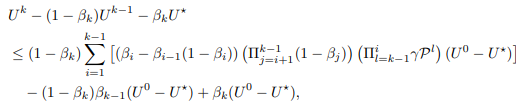
\ and let U¯ be the entire right hand side of inequality. Then, we have

\

\ Now, we prove the second rates of Theorem 2.

\

\

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\