and the distribution of digital products.
Apparate: Early-Exit Models for ML Latency and Throughput Optimization - Latency-Focused Adjustments
:::info Authors:
(1) Yinwei Dai, Princeton University (Equal contributions);
(2) Rui Pan, Princeton University (Equal contributions);
(3) Anand Iyer, Georgia Institute of Technology;
(4) Ravi Netravali, Georgia Institute of Technology.
:::
Table of Links2 Background and Motivation and 2.1 Model Serving Platforms
3.1 Preparing Models with Early Exits
3.2 Accuracy-Aware Threshold Tuning
3.3 Latency-Focused Ramp Adjustments
5 Evaluation and 5.1 Methodology
5.3 Comparison with Existing EE Strategies
7 Conclusion, References, Appendix
3.3 Latency-Focused Ramp AdjustmentsThe set of active ramps ultimately dictates where inputs can exit, and thus provides bounds on potential latency savings. Unlike threshold tuning which runs reactively (since accuracy is a constraint) and uses only recent profiling data to evaluate new configurations, ramp adjustment is strictly an optimization (for latency savings), and requires deployment to evaluate the impact of any new ramp. Thus, Apparate’s ramp tuning runs periodically (every 128 samples by default) and conservatively alters the set of active ramps to incrementally converge on high-performing configurations.
\ Evaluating active ramps. In each round, Apparate’s controller starts by computing a utility score for each active ramp that evaluates its overall impact on workload latency. To do so, Apparate couples per-ramp exit rates (based on profiling data from threshold tuning in §3.2) with two additional inputs that are collected once per model during bootstrapping: (1) the latency overhead per ramp, and (2) a layerwise breakdown of time spent during model inference (for different batch sizes [22]). The latter is necessary since different models can exhibit wildly different latency characteristics that govern the impact of any exits. For instance, latency of CV models is often heavily skewed towards early layers given the high dimensionality of the input data [40], while NLP transformers exhibit more consistent latency values across coding blocks. Note that, in the case of distributed serving, latency breakdowns are updated to account for network delays between serving nodes.
\ Using these inputs, Apparate defines the utility of ramp R as savings - overheads, where savings represents the sum of raw latency that exiting inputs avoided by using ramp R, and overheads is the sum of raw latency that R added to inputs that it was unable to exit. A negative (positive) utility value means a ramp is causing more (less) harm than benefit to overall latencies for the current workload.
\ Adding new ramps. If any negative utility values exist, Apparate applies a fast threshold tuning round to see if ramp utilities become entirely positive without harming overall latency savings. If not, Apparate immediately deactivates all negative-utility ramps. From there, the key question to address is what ramps (if any) should be added to make use of the freed ramp budget. The main difficulty is in predicting the utility of each potential addition. Indeed, while per-exit latency savings for each potential ramp are known (using the latency breakdown from above), exit rates are not.
\ To cope with this uncertainty, our guiding intuition is that, subject to the same accuracy constraint, later ramps almost always exhibit higher exit rates than earlier ones. [2] The reason is that late ramps have the luxury of leveraging more of an original model’s computations when making a prediction. Importantly, this implies that a candidate ramp’s exit rate is bound by the exit rate of the closest downstream ramp.
\ Building on this, Apparate’s controller computes an upper bound on the utility of candidate ramps as follows. To avoid inter-ramp dependencies harming ramps that are already performing well, we only consider additions after the latest positive ramp P in the model. In particular, Apparate divides the range following P into intervals separated by any negative ramps deactivated in this round. The first round of candidate ramps are those in the middle of each interval.
\
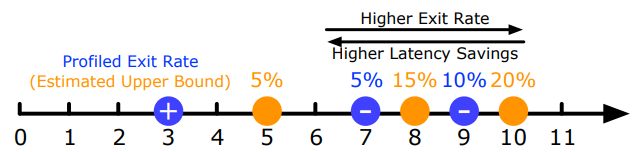
\ For each candidate ramp, we compute its upper-bound exit rate as the sum of profiled exit rates for the following deactivated ramp and any earlier deactivations (Figure 12); the idea is that inputs from earlier deactivations would have reached the following deactivated ramp and might have exited there. Utility scores are then computed as above, and the ramp with the highest positive utility score is selected for trial. If all ramps have negative projected utilities, Apparate repeats this process for later candidate ramps in each interval. Once a ramp is selected for trial, Apparate adds it to the deployed model definition, while removing deactivated ramps. Trialed ramps start with threshold=0 to prevent inaccurate exiting, but are soon updated in the next round of threshold tuning.
\ Until now, we have only discussed how Apparate handles scenarios with at least one negative ramp utility. In the event that all ramps exhibit positive utilities, Apparate enters a lowrisk probing phase to determine if latency savings can grow by injecting (or shifting to) earlier ramps. There are two scenarios for this. If ramp budget remains, we add a ramp immediately before the existing ramp with highest utility (while keeping that ramp to preserve its exiting wins). In contrast, if no ramp budget remains, we shift the ramp with the lowest utility score one position earlier, leaving the most positive ramp untouched. Additions are incorporated into the configuration using the same process as above.
\
:::info This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.
:::
[2] For a single input, being able to exit at an early ramp does not guarantee exit capabilities at later ramps [34]. However, later-ramp exit rates were always higher than earlier ones for our workloads, and we note that Apparate only uses this property for search efficiency, not correctness.