Anchor Data Augmentation (ADA): A Domain-Agnostic Method for Enhancing Regression Models

:::info Authors:

(1) Nora Schneider, Computer Science Department, ETH Zurich, Zurich, Switzerland ([email protected]);

(2) Shirin Goshtasbpour, Computer Science Department, ETH Zurich, Zurich, Switzerland and Swiss Data Science Center, Zurich, Switzerland ([email protected]);

(3) Fernando Perez-Cruz, Computer Science Department, ETH Zurich, Zurich, Switzerland and Swiss Data Science Center, Zurich, Switzerland ([email protected]).

:::

Abstract and 1 Introduction

2 Background

2.1 Data Augmentation

2.2 Anchor Regression

3 Anchor Data Augmentation

3.1 Comparison to C-Mixup and 3.2 Preserving nonlinear data structure

3.3 Algorithm

4 Experiments and 4.1 Linear synthetic data

4.2 Housing nonlinear regression

4.3 In-distribution Generalization

4.4 Out-of-distribution Robustness

5 Conclusion, Broader Impact, and References

\ A Additional information for Anchor Data Augmentation

B Experiments

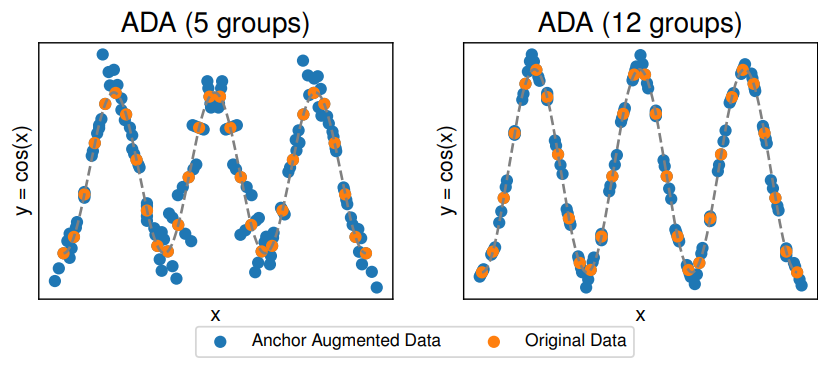
In this section, we introduce Anchor Data Augmentation (ADA), a domain-independent data augmentation method inspired by AR. ADA does not require previous knowledge about the data invariances nor manually engineered transformations. As opposed to existing domain-agnostic data augmentation methods [10, 45, 46], we do not require training of an expensive generative model, and the augmentation only adds marginally to the computation complexity of the training. In addition, since ADA originates from a causal regression problem, it can be readily applied to regression problems. Even when ADA does not improve performance, its effect on performance remains minimal.

\

\

\

\

\

:::info This paper is available on arxiv under CC0 1.0 DEED license.

:::

\