The Algorithm for Inserting Sequences into Sequences

\ In software development, ==ordered data sequences== are needed practically everywhere, from displaying products in an online store and tracking orders to managing messages in a chat or handling task priorities in project management tools. Now, the challenge arises when data needs modifications. You need to maintain the correct order, and keeping it that way when inserting, deleting, or rearranging elements can become complex, particularly when using traditional numbering systems.

\ One problem I have seen time and time again is ==the need to insert an ordered sequence of elements== between two existing ones in a dataset. Traditional approaches don't quite cut it, especially when dealing with enormous datasets, and I’d like to offer you a solution. I’ve spent a while perfecting an approach that would help avoid the performance bottlenecks that come with recalculating sequence numbers – and here it is, an alternative algorithm that simplifies this task by ==leveraging a string-based ordering system.==

Typically, to maintain order in a sequence, a special parameter is assigned to the elements of a sequence, often called a "sequence number," which determines the order of a specific component – be it a product, document, message in a chat, order, etc. – in the final sequence.

\ It’s one thing to simply display elements in a given order, but it’s another to maintain that order when inserting, deleting, or modifying elements. A usual scenario is when we need to insert an ordered sequence of elements into an already ordered sequence. For example, we might want to insert ten elements between the fifth and sixth elements. If the sequence uses natural numbers for ordering (i.e., the first element has a sequence number of 1, the second has 2, the third has 3, and so on), then to insert a sequence of ten elements between the fifth and sixth elements, we would need to somehow "spread" the natural number range. This contradicts the definition of natural numbers, as there can’t be anything between two consecutive numbers in a natural number series.

\ \

\ There are two possible solutions to this problem:

\ Option 1: We assign the new elements the numbers 6, 7, 8, …, 15, and for the elements that were originally numbered 6 and higher, we simply add 10 to their numbers, making them 16, 17, 18, and so on. This shifts everything after the insertion point.

\

\n Option 2: We move from natural numbers to real numbers. In this case, we can insert fractional numbers between the fifth and sixth elements, like this: 5, 5.1, 5.2, 5.3, …, 5.10, 6.

\

Both of these have their downsides, which can often be significant enough to make you reconsider your choice. For example, switching from natural numbers to real numbers comes with the problem of limited precision: we can only make a finite number of insertions before running into the limits of floating-point accuracy. A number like 5.127956 has a finite sequence of digits after the decimal point, meaning we can’t keep inserting numbers indefinitely.

\ The approach of using natural numbers as sequence numbers and shifting the entire sequence when inserting another ordered sequence also has its own set of problems. The first issue is that such an insertion will require recalculating all previously assigned sequence numbers. If we’re dealing with large datasets (thousands, hundreds of thousands, or even millions of items) and we make an insertion near the beginning of the list, we’ll have to shift all (and I mean, all) of the sequence numbers, which can affect performance in a way we certainly don’t want it to. Plus, we would need to lock the database during the process of updating such a large volume of data, as we’re essentially performing a massive update operation.

\ And before you say anything, yes, there are ways to handle the challenges of large-scale operations. However, I want to discuss an approach that avoids the need for such mass updates altogether. Reserve those heavy-duty tools for more complex tasks where you won't be able to avoid mass operations.

Before we rush to a solution, let's think this through: how can we insert 10 elements between the numbers 5 and 6, using natural numbers? One initial approach could be to always insert new elements with some spacing between them, so we never run into a situation where we need to insert elements between, say, 5 and 6. For example, when we first insert elements (let’s say 5 of them), instead of numbering them 1, 2, 3, 4, 5, we could number them 100, 200, 300, 400, and 500. This creates a "gap" that allows us to insert elements between the fifth and sixth positions, which now have sequence numbers 500 and 600. This way, we could easily insert up to 100 elements between 500 and 600 without any issues.

\ However, this comes with three main problems:

\

1. We need to predict how large the gap should be.

   \

2. Hitting the maximum value for integers happens much quicker than you would expect. If we keep creating large gaps between numbers, we will eventually run into a situation where even after inserting a small number of elements, we reach an excessively large number, beyond the range that modern data types can store.

   \

3. Limited space. As we continue making insertions, we are gradually filling in our initially spaced-out sequence, making it denser and denser. Eventually, we’ll end up with two natural numbers (e.g., 500 and 501) between which nothing can be inserted.

So, we come to realize that neither natural numbers nor real numbers can fully solve this problem for us. However, numbers – whether natural or real – are fortunately not the only way or data type that can be ordered. One such type is strings. Most modern and popular programming languages and database management systems can compare strings, allowing us to order them using lexicographic order based on ASCII character codes.

\ Now let's get to the point. For simplicity, we’ll take only the characters from A to Z and a to z from the ASCII set. Then, we choose a word length, say 3, and call a word with three characters a "domain". For example, AAA would be the first domain (because the character A has the smallest ASCII code), and zzz would be the last. This gives us a sequence of domains: AAA, AAB, …, ZZZ, aaa, aab, …, zzz. This sequence contains (26 uppercase letters + 26 lowercase letters)³ = 140,608 words, which allows us to arrange 140,608 elements in order.

\ Then, we need to calculate the "left" and "right" words, when inserting new elements. These correspond to the words of the elements on the left and right (in the examples earlier, these were the fifth and sixth elements). If there is no left or right word (as in the case of the first insertion, or an insertion at the beginning or end), the smallest domain (AAA) is used as the left word, and the largest domain (zzz) is used as the right word.

\ After that, elements are inserted one by one, with their ordinal number assigned based on the formula: left word + 1. The "+1" refers to the next word in lexicographical order, which is calculated as the next permutation with repetition. The insertion proceeds if the left word + 1 is still less than the right word. Otherwise, the ordinal number is calculated using the formula: left word + the smallest domain. After this, the left word is updated to the word that was just inserted.

\ To clear this up, let's look at an example of inserting the first 3 elements into an initially empty sequence:

\n Determine the left and right words. Since the sequence is empty, the left and right words are AAA and zzz, respectively.

\

1. Insert the first element. Its ordinal number is AAA + 1 = AAB. Is AAB less than zzz? Yes, so we go on. The left word now becomes AAB.
2. Insert the second element. Its ordinal number is AAB + 1 = AAC. Is AAC less than zzz? Yep, good. The left word now becomes AAC.
3. Insert the third element. Its ordinal number is AAC + 1 = AAD. Is AAD less than zzz? Yes? Great, this works out.

\ After this, your sequence will be AAB, AAC, AAD. Now you can insert two elements between AAB and AAC.

\

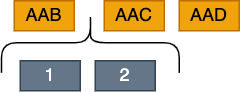
\ This is where things get interesting. When we insert the first element after the left word (AAB), AAB + 1 gives us AAC, which is equal to the right word (AAC). This is exactly why we introduced the concept of a "domain" – instead of adding +1, we add the smallest domain, which in our case is AAA. So, the result would be AAB_AAA (I've added the underscore here for readability in the article, but you could also use it to enhance readability when debugging the algorithm).

\ Next, when inserting the second element, we add +1 to AABAAA, which gives us AABAAB, and this is definitely less than AAC. This means we now have space to insert 140,608 whole more elements!

\ The final sequence is now this: AAB, AABAAA, AABAAB, AAC, AAD.

\ It maintains the order when sorted and is also derived from the previous one without changing the ordinal numbers of the elements that were already in the sequence before the insertion. Do you know what this means? We've solved the main issue of inserting into an ordered sequence!

At first glance, it might seem similar to the approach with spaced-out natural numbers, where we need to decide what domain length will work for us. However, in this case, even if we choose a domain length of one, we would simply concatenate domains more frequently. This doesn't affect the complexity of the algorithm or the final result. But if we want "cleaner" or "prettier" strings in our database, we can increase the initial domain length to reduce the number of concatenations. So, if we increase the domain length to 4, we could order up to 7,311,616 elements using just a single domain.

\ However, our most attentive readers might have noticed that the above algorithm would break down if we inserted an element between AAB and AABAAA. If we add +1 to AAB, we get AAC, which is greater than AABAAA. And if we add the smallest domain, we get AAB_AAA, but this element already exists and is the “right” word.

\ No worries, this can be solved too. Instead of inserting the smallest domain, insert the "middle" domain, the one that lies in the middle of the domain sequence. In our case, the sequence is even, so we can choose either ZZZ or aaa (which is what we'll do moving forward). Alternatively, we could choose a character from the ASCII table that comes after Z but before a, such as the symbol ^. This way, each new domain insertion opens the possibility to insert elements around it, allowing us to use half of the domain's capacity at the given length K (in our case, K equals 3, and with an alphabet of 52 symbols, the domain capacity is 140,608 elements, so half of that would be 70,304).

\ And after inserting such a domain, elements are added either from the left word or from the right ("backwards") as follows:

\

1. Insert an element between AAB and AAC.

   \

2. Check if there are available spots without introducing a new domain — either to the right of the left word or to the left of the right word. If there’s space to add on the right side of the left word without creating a new domain, we increment the left word by +1 and continue adding from the right of the left word. If space is available to add on the left side of the right word without creating a domain, we choose it and decrement the right word by -1. If neither side has space, we create a new domain.

   \

3. In this case, since neither the right side of AAB nor the left side of AAC has space, we add a domain: AAB + "middle domain" = AABaaa. This gives us AAB, AABaaa, AAC.

   \

4. Now, in this setup, we can insert up to 70,304 words on either side of AAB_aaa.

\

\ However, it’s essential to avoid getting too close to AABAAA or AABzzz, as this would again prevent any further insertions between AAB and AABAAA or between AABzzz and AAC.

\

\

\ If you reach the last available space (when no further +-1 operations are possible), instead of filling that space, just create a new domain straight away. So, instead of inserting the word AABAAA, insert AABAAA_aaa.

\ \ \n

Lastly, we can also make the very first insertion relative to the middle of the domain (aaa) instead of AAA/ZZZ. This makes our algorithm even more generic, as we can treat an empty sequence as something where no insertions are possible without first adding a domain. This, in turn, leads to the creation of the first domain – aaa.

\ Congratulations! We've found a solution to one of the most common challenges in handling ordered sequences. Now you can organize sequences, change the order of their elements, and perform insertions and deletions without the need to recalculate the entire sequence. Only the new elements will receive new ordinal numbers (represented as strings) in the database. This means that any insertion into any part of the sequence will not trigger a recalculation of all the ordinal numbers, as would be required if we used the classic approach with natural numbers.

\ You won’t have to worry about performance drops anytime soon, even when handling large volumes of ordered data. The problem is solved, and now you can take a breather before tackling the next seemingly endless dataset. The best part? You’ve got a new tool in your toolkit!